Очень значимую роль в анализе явлений микромира имеет принцип Паули. Данное предположение Паули выдвинул еще до возникновения квантовой механики. Паули сформулировал его относительно электронов:
В атоме не может быть двух электронов, которые бы характеризовались одинаковыми четверками квантовых чисел $(n,l,m_l,\ m_s)$, то есть в одном и том же состоянии не может находиться больше, чем один электрон.
Так, если два электрона имеют одинаковые главные квантовые числа $(n)$ и орбитальные числа совпадают, то спины их должны быть ориентированы противоположно (то есть их квантовые числа $m_s\ равны\ \frac{1}{2}\ и-\frac{1}{2}$).
Математическая запись принципа Паули
Рассмотрим систему из двух электронов. Если взаимодействие электронов не учитывать, то волновой функцией движения электрона в пространстве можно считать:
где индексы $a\ и\ b$ обозначают состояния электронов условно имеющих номера $1$ и $2$. Полная функция для $2$ электронов есть произведение спиновой волновой функции на волновую функцию их движения в пространстве. Спиновые волновые функции запишем как:
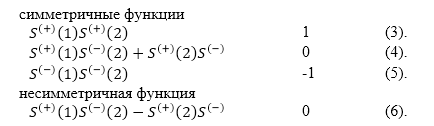
Рисунок 1.
В результате умножений получается восемь разных полных волновых функций, имеющих симметрию. При этом имеем: произведение двух симметричных и двух антисимметричных функций дает симметричную функцию. Умножение симметричной функции на антисимметричную -- антисимметричная функция. В результате получаем, что у нас из восьми полных волновых функций $50\%$ симметричные:
К антисимметричным функциям отнесем:
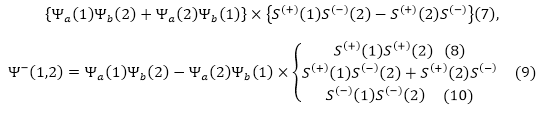
Рисунок 2.
Симметричные функции:
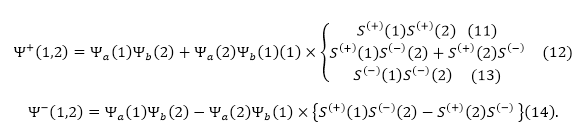
Рисунок 3.
Не все из записанных выше \Psi -- функций возможны, если следовать принципу Паули. Если квантовые числа двух электронов равны, то волновая функция становится равной нулю. Допустим, электроны совершают одинаковое движение по орбитам ($a=b$). В таком случае (по принципу Паули) возможна только противоположная ориентация спинов электронов. волновые функции, которые относятся к описанию ориентации спина в одно направлении (8-10) становятся равными нулю, так как нулевым является первый множитель. Волновая функция (7) не равна нулю, она описывает противоположные спины. Получается, что при $a=b$ антисимметричные волновые функции согласуются с принципом Паули.
Рассмотрим вторую группу волновых функций (11-14). При $a=b$ симметричные функции при одинаковой ориентации спинов не становятся равны нулю. Следовательно, они не допустимы. Функция (14) описывает поведение электронов спины который ориентированы противоположно, это значит, что она могла бы быть не равна нулю. Однако при $a=b$ первый множитель рассматриваемой функции равен нулю, получается, что \Psi-функция в таких случаях всегда равна нулю, что не совместимо с принципом Паули, который в этом случае разрешает состояния с разными спинами. Делаем вывод, что симметричные функции неприемлемы.
Опираясь на приведенные рассуждения, сформулируем принцип Паули:
Полная волновая функция двух электронов должна быть антисимметричной функцией относительно перестановки электронов. Так как формулы (7) - (14) были записаны без учета взаимодействия электронов, но при рассуждениях использовались исключительно свойства симметрии $\Psi$ -- функций, которые связаны с тождественностью электронов и не зависят от их взаимодействия (Если учесть взаимодействие электронов, то обменное вырождение отсутствует, но свойства симметрии волновых функций остается, так как тождественность частиц сохраняется и при их взаимодействии.), то все выводы отнесем и к взаимодействующим электронам.
В случае если следует иметь дело с большим, чем $2$ количеством электронов, данное выше утверждение можно обобщить и формулировать как:
Волновая функция совокупности электронов должна быть антисимметричной функцией относительно перестановки любой пары электронов:
Применение принципа Паули
Данный принцип использовался для обоснования периодической системы Менделеева, части закономерностей в спектрах.
Так, в основе строения электронных оболочек атома лежат два принципа:
-
Принцип Паули. Он учитывает квантовые свойства возможных состояний атома.
-
Принцип минимума энергии: при данном суммарном количестве электронов в атоме реализуется состояние с минимальной энергией. Это требование является естественным относительно устойчивости атома.
Анализируя строение атома в первом приближении энергией взаимодействия электронов пренебрегают. Считают, что сумма энергия атома равна сумме энергий электронов в поле ядра, которая известна. Значит, не составляет особого труда определить каково распределение электронов по разным состояниям, принимая во внимание принцип Паули. Получается схема заполнения оболочек, которая, надо отметить, все же отличается от реальной, но является полезной.
В зависимости от значения орбитального квантового числа $l\ $состояние электрона в атоме обозначают разными буквами. Значениям $l=0,1,2,3,4,5\dots $ ставятся в соответствие буквы $s,p,d,f,g,h$ и по алфавиту.
Распределение электронов по состоянию в атоме записывают при помощи спектроскопических символов (Табл.1):
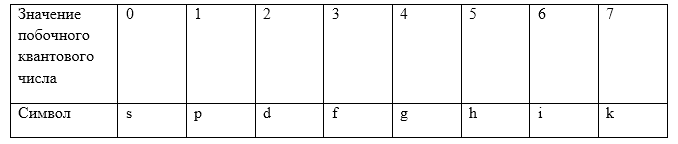
Рисунок 4.
Электронную структуру записывают так: число, находящееся слева -- главное квантовое число $(n)$, сам спектроскопический символ соответствует величине орбитального квантового числа $(l)$.
Примените принцип Паули, ответьте на вопрос: какое максимальное количество электронов $N_{max}$ в атоме могут иметь одинаковые квантовые числа 1) $n,l,m_l,m_s$; 2) $n$?
Решение:
Состояние электрона в атоме определено однозначно совокупностью четырех квантовых чисел:
- главного $n\ (n=1,2,3...),$
- орбитального$\ l\ (l=0,1,2,...,n-1)$,
- магнитного $m_l$ ($m_l=-l,\dots ,\ -1,0,1,\dots ,l$),
- магнитного спинового $m_s$($m_s=\pm \frac{1}{2}$).
1) Согласно принципу Паули один электрон в атоме может иметь определенную совокупность квантовых чисел $n,l,m_l,m_s.$
2) При заданном главном квантовом числе ($n$) орбитальное квантовое число ($l$) может принимать значения от $0$ до $n-1$, при этом каждому значению $l$ соответствует $2l+1$ разных величин $m_l$, в таком случае количество разных состояний, которые соответствуют известному главному квантовому числу равно:
\[\sum\limits^{n-1}_{i=0}{\left(2l+1\right)=n^2}.\]Квантовое число $m_s$ может иметь только два значения, значит максимальное количество электронов, которые имеют одинаковые главные квантовые числа, может быть равно:
\[N_{max}=2n^2.\]Ответ: 1) $N_{max}=1$, 2)$\ N_{max}=2n^2.$
Электронный слой, характеризуемый главным квантовым числом равным $n=3$, полностью заполнен. Какое количество электронов имеют одинаковые магнитные квантовые числа равные $m_l=2$?
Решение:
В соответствии с ответом $2$ примера $1$ мы можем сказать, что при $n=3$ в атоме может существовать $18$ электронов. При этом $l=0,1,2;;$ $m_l=0,\pm 1,\pm 2;\ m_s=\pm \frac{1}{2}$. Распределение электронов удобно свести в таблице (Табл.2):
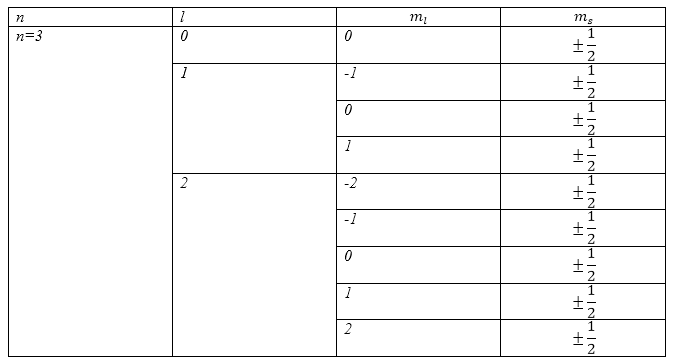
Рисунок 5.
Из таблицы видно, что для пары квантовых чисел $n=3$,$\ m_l=2$ имеется два электрона.
Ответ: Два электрона.











