Символ терма включает информацию о таких квантовых числах как: полный спиновый угловой момент (полное спиновое квантовое число) ($S$), полный орбитальный угловой момент атома (полное орбитальное квантовое число) ($L$), полный момент количества движения атома ($J$). Напомним, что
Векторам $\overrightarrow{J},\overrightarrow{L},\overrightarrow{S}$ соответствуют квантовые числа $J,L,S$. $\overrightarrow{S}=\sum{{\overrightarrow{s}}_i},\ \overrightarrow{L}=\sum{{\overrightarrow{l}}_i}.$
Символ терма записывают как:
где величина $2S+1$ указывает спиновую мультиплетность состояния, $L$ -- квантовое число орбитального момента, которое записывается при помощи обозначений буквами $(S,P,D...)$, $J$ -- квантовое число полного углового момента, который вызван взаимодействием спинового и углового орбитальных моментов. Для атомов, которые имеют несколько электронов числа $L$ и $S$ являются приближенными, причем, чем больше атомный номер элемента, тем хуже приближение. Эти квантовые числа не являются измеряемыми напрямую. Единственной наблюдаемой величиной является полный угловой момент $J$. Если электронная конфигурация атома задана, то символ терма, который индивидуализирован, соответствует состоянию с определенной энергией.
Значения $J$ определяют, разделяя два вида схемы связи. В том случае, если взаимодействием спинового и орбитального моментов можно пренебречь в сравнении с отталкиванием электронов (например, у атомов легких элементов) ($L-S$ взаимодействие), то:
- находят полный орбитальный момент, используя формулу ($\overrightarrow{L}=\sum{{\overrightarrow{l}}_i})$ и орбитальные моменты отдельных электронов;
- вычисляют полные значения $\overrightarrow{S}=\sum{{\overrightarrow{s}}_i}$ по одноэлектронным спиновым моментам;
- затем полное значение $J$ находят как сумму $\overrightarrow{J}=\overrightarrow{L}+\overrightarrow{S}.$
Для атомов тяжелых элементов применяется схема $j-j$ взаимодействия. В данном случае спин-орбитальным взаимодействием пренебречь нельзя. В таком случае, используя значения $l\ и\ s$ для каждого отдельного электрона, вычисляют величину $j$. После этого проводят суммирование всех $$ и получают $J$. .
Относительная устойчивость термов
Правило Гунда
Данное правило позволяет определять относительную устойчивость разных термов, которые возникают при заданной электронной конфигурации. В соответствии с этим правилом самым устойчивым состоянием, которое может возникнуть из заданной конфигурации является то, которое имеет максимальную спиновую мультиплетность.
Правило для орбитального момента ($L$) и полного углового момента ($J$)
Данные правила выполняются только для основного состояния атомов. При заданной величине $S$ основное состояние всегда характеризуется максимальным значением $L.$
Значение квантового числа $J$ для основного состояния зависит от заселенности незамкнутой оболочки. Если имеется только одна незамкнутая оболочка, и она заполнена менее чем на половину, самому низшему энергетическому состоянию соответствует минимальное значение $J$. В том случае, если исследуемая оболочка заполнена более чем на половину, о низшее по энергии состояние характеризуется максимальным значением $J$. Если оболочка имеет заполнение ровно $\frac{1}{2}$, то $L=0$. В таком случае, если $L=0,\ S=S_{max}$, то $J$ имеет единственно возможное значение. Правило, которое определяет значение $J$, выполняется не всегда, если незамкнутых оболочек больше, чем одна.
Энергии основных термов
Для конкретной конфигурации электронов можно иногда можно построить ряд атомных термов, которые имеют разную энергию. Терм может расщепляться на мультиплет, образовывая тонкую структуру. Часто требуется выделить основной терм и основное состояние.
Для основного состояния атомов существуют эмпирические правила, которые называют правилами Хунда:
- Если задана электронная конфигурация, то минимальную энергию имеет терм, полный спин ($S$) которого является самым большим (мультиплетность максимальна).
- Если имеется несколько термов с одинаковой мультиплетностью, то самым низким является тот терм, у которого самое большое значение полного орбитального момента ($L$).
Правила Хунда объясняют тем, что при максимальных величинах $S$ и $L$ электроны (в среднем) располагаются дальше друг от друга. Значит, энергия отталкивания минимизируется.
Так, рассмотрим электронную конфигурацию $d^2.$ Можно определить каким является основной терм для такой конфигурации не находя полный набор термов. Для того, чтобы выполнялось первое правило Хунда и S было равно максимальному значению, то есть единице необходимо, чтобы имеющиеся два электрона в приведенной конфигурации имели одинаковую проекцию спинов (либо $+\frac{1}{2},\ либо-\frac{1}{2}\ $). При этом состояния электронов должны быть таковы, что полный орбитальный момент был максимальным. Так как значение $L=4$ было бы не совместно с требованием $S=1$ (электроны были бы спаренными), значит $L=3$. Получаем, что основным будет терм ${}^3F$.
Для выявления основного состояния в терме применяют правило Ланде (иногда оно включено в правила Хунда):
если подоболочка атома заселена меньше, чем на $\frac{1}{2}$, то минимальной энергией обладает нормальный мультиплет (состояние, которое имеет минимальное значение $J$); ели подоболочка заполнена более, чем на 50\%, то минимальную энергию имеет состояние с максимальным $J$ (обращенный мультиплет).
Задание: Определите основной терм атома азота.
Решение:
Атом азота имеет электронную конфигурацию:
\[1s^22s^22p^3.\]Пусть спины всех внешних электронов (их количество равно трем) направлены в одну сторону. Следовательно, получим:
\[S_{max}=\frac{3}{2},\]что означает, что у нас имеется квартетный терм. Составим таблицу из квантовых чисел:
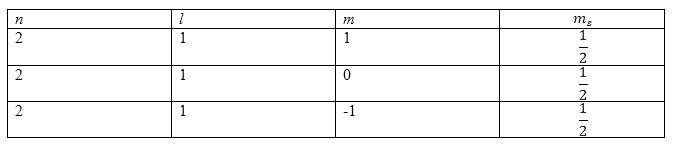
Рисунок 1.
Для того, чтобы все спины имели одинаковые направления необходимо использовать все величины магнитного квантового числа ($m$). Получим, что:
\[L_{max}=0.\]Ответ: Можно сделать вывод о том, что основным термом является терм ${}^4S$, а основное состояние - ${{}^4S}_{\frac{3}{2}}.$
Задание: Каким будет основной терм атома кислорода?
Решение:
Атом кислорода имеет электронную конфигурацию:
\[1s^22s^22p^4.\]Составим таблицу из квантовых чисел:

Рисунок 2.
Для атома кислорода нельзя направить все спины в одну сторону. В результате видно, что получаем два некомпенсированных спина. Значит, основной терм будет триплетом. Помимо этого результирующий орбитальный момент равен:
\[L=1.\]В качестве основного терма имеем:
\[{}^3{P.}\]Применим правило Ланде, учтем, что p -- подоболочка заселена более чем на $\frac{1}{2}$, получим основное состояние:
\[{{}^3P}_2.\]Ответ: Основной терм кислорода - ${}^3{P,}\ $основное состояние - ${{}^3P}_2.$











