Закон Джоуля Ленца в интегральной форме
Форма энергии, которая выделяется при прохождении по проводнику электрического тока, зависит от природы физических факторов, которые вызывают падение потенциала. Так, например, изменение потенциала на сопротивлении проводов сопровождается выделением тепла, падение напряжения на клеммах двигателя постоянного тока связано с производством механической работы.
Допустим, что участок цепи -- неподвижный проводник. Вся работа тока превращается в тепло, которое на проводнике выделяется. Если проводник однороден, подчиняется закону Ома:
где $R$ -- сопротивление проводника, то можно записать, что работа (А) электрического тока равна:
где $t$ -- время прохождения током рассматриваемого проводника, то вся выделенная на проводнике энергия в виде тепла равна:
Формула (3) есть закон Джоуля -- Ленца в интегральной форме. Этот закон открыт в 1841 г. Джоулем и позднее Ленц подробно исследовал его.
В том случае, если сила тока не постоянна во времени, то количество тепла, которое выделяется на проводнике можно рассчитать в соответствии с формулой:
Необходимо отметить, что эффект нагревания проводника током находит применение на практике. Наиболее известное из них -- лампы накаливания.
Закон Джоуля - Ленца в дифференциальной форме
Над электроном, который движется в проводнике со скоростью $\overrightarrow{v'}=\left(\overrightarrow{v}+\overrightarrow{u}\right),$ где $\overrightarrow{v}$ -- скорость теплового движения молекул, $\overrightarrow{u}$ -- скорость упорядоченного движения носителей тока при наличии поля за единицу времени (t=1с), совершается работа равная ($A_q$):
Примем, что $\overrightarrow{F}$=const, усредним выражение (4), получим:
где $\left\langle \overrightarrow{v}\right\rangle $=0. Если через n- обозначим концентрацию электронов, то работа над электронами в единице объема металла ($A'$) за единицу времена равна:
где $\overrightarrow{j}$ -- плотность тока, $\sigma $ -- удельная проводимость проводника.
В металлах эта работа идет на приращение внутренней энергии, так как прохождение электрического тока по проводнику не сопровождается изменением структуры металла. Значит, можно записать, что удельное количество тепла (удельная мощность тепловыделения) $Q_{ud}$, которое выделяется на проводнике в единице объема за единицу времени равно:
Формула (8) закон Джоуля -- Ленца в локальной (дифференциальной) форме. В форме (8) данный закон не зависит от природы сил, которые порождают ток, значит, в такой формулировке носит общий характер. В том случае, если сила, которая действует на электроны исключительно электрической природы, то есть:
выражение (8) можно представить как:
Закон Джоуля -- Ленца справедлив и для электролитов. Что означает, работа электрического поля не тратится на образование ионов. Ионы в растворе образуются в результате диссоциации молекул, когда происходит процесс растворения.
Задание: Электрический ток проходит по спирали с сопротивлением R. Ток равномерно убывает до нуля за время $\triangle t$. За обозначенный период времени через спираль проходит заряд q. Какое количество тепла выделится на спирали за данный промежуток времени?
Решение:
В качестве основы для решения задачи примем закон Джоуля Ленца в виде:
\[Q=\int\limits^t_0{I^2Rt}\left(1.1\right).\]Из определения силы тока запишем:
\[I=\frac{dq}{dt}\ \left(1.2\right),\]следовательно, заряд, который проходит через проводник, равен:
\[q=\int\limits^{t_2}_{t_1}{Idt}\left(1.3\right).\]В условии задачи сказано, что ток убывает равномерно, следовательно, закон убывания тока ищем в виде:
\[I=at+b\left(1.4\right),\]где $a,b$ постоянные. За начальный момент времени примем $t_1$=0, тогда $t_2=\triangle t.\ $Подставим (1.4) в (1.3) проведем интегрирование:
\[q=\int\limits^{\triangle t}_0{\left(at+b\right)dt=a\frac{{\triangle t}^2}{2}}+b\triangle t\left(1.5\right).\]По условию задачи в некоторый момент времени $t_2$ ток стал равен нулю, то есть:
\[I=a\triangle t+b=0\ \left(1.6\right),\]Получим:
\[b=-a\triangle t(1.7)\]Найдем коэффициент a из (1.5), учитывая (1.7):
\[q=a\frac{{\triangle t}^2}{2}-a\triangle t\triangle t=\frac{a}{2}{\triangle t}^2\to a=\frac{2q}{{\triangle t}^2}\left(1.8\right).\]Подставим (1.8) в (1.1), получим искомое тепло:
\[Q=\int\limits^{\triangle t}_0{{\left(at+b\right)}^2Rdt}=R\int\limits^{\triangle t}_0{\left(a^2t^2+2abt+b^2\right)dt=}R\left(\frac{a^2{\left(\triangle t\right)}^3}{3}+2ab\frac{{\left(\triangle t\right)}^2}{2}+b^2\triangle t\right)\left(1.9\right)\] \[Q=R\left(\frac{{\left(\frac{2q}{{\triangle t}^2}\right)}^2{\left(\triangle t\right)}^3}{3}+2\frac{2q}{{\triangle t}^2}\left(-\frac{2q}{{\triangle t}^2}\triangle t\right)\frac{{\left(\triangle t\right)}^2}{2}+\left({\left(-\frac{2q}{{\triangle t}^2}\right)}^2{\triangle t}^2\right)\triangle t\right)=R\left(\frac{4q^2}{3\triangle t}-\frac{4q^2}{\triangle t}+\frac{4q^2}{\triangle t}\right)=\frac{4q^2}{3\triangle t}R.\]Ответ: Q=$\frac{4q^2}{3\triangle t}R.$
Задание: Сравните удельную мощность тепловыделения электрического поля для сечений $S_1$ и $S_2$ (рис.1) проводника. Если по проводнику течет постоянный ток ($I=const$).
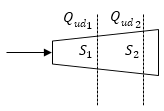
Рис. 1
В качестве основания для решения используем локальную формулировку закона Джоуля Ленца:
\[Q_{ud}=\frac{1}{\sigma }j^2\left(2.1\right).\]Для проводника в месте сечения $S_1$ можно записать, что:
\[j_1=\frac{I}{S_1}\left(2.2\right).\]Для проводника в месте сечения $S_2$ можно записать, что:
\[j_2=\frac{I}{S_2}\left(2.3\right).\]Тогда формула (2.1) преобразуется к виду:
\[Q_{ud1}=\frac{1}{\sigma }{\left(\frac{I}{S_1}\right)}^2\left(2.4\right),\] \[Q_{ud2}=\frac{1}{\sigma }{\left(\frac{I}{S_2}\right)}^2\left(2.5\right).\]Мы получили, что удельное количество тепла обратно пропорционально площади сечения проводника.
Ответ: $Q_{ud1}>Q_{ud2}$.












