Определение
Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):
Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.
Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.
Иногда модуль вектора индукции однородного магнитного поля определяют как:
где $M_{max}$ -- максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ -- магнитный момент контура ($S$- площадь контура). За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.
Очень часто, определение для вектора магнитной индукции записывают в виде:
где $\overrightarrow{dF}$ -- сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:
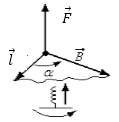
Рис. 1
Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:
Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).
Принцип суперпозиции вектора индукции магнитного поля
Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:
Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:
Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.
Решение:
Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.
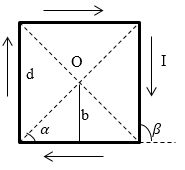
Рис. 2
В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:
\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:
\[B=4B_1\left(1.2\right).\]В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:
\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1.3\right),\]углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):
\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:
\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$
Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.
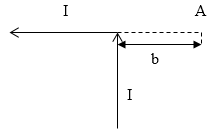
Рис. 3
Решение:
В точке А поле создается двумя частями проводника:
\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]Рассмотрим горизонтальный участок, на продолжении которого лежит точка А. Этот участок проводника с током создает поле в точке А индукция $(\overrightarrow{B_{II}})$которого, равна нулю, так как в точке А углы между всеми элементами с током и радиус-векторами будут равны $\pi .\ $Следовательно, векторное произведение ($\left[d\overrightarrow{l}\overrightarrow{r}\right]$), в законе Био -- Савара -- Лапласа равно нулю:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\oint{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\left(2.2\right),\]где $\overrightarrow{r}$ -- радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).
Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:
\[B'=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:
\[{B=B}_{\bot }=\frac{1}{2}B'=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$











