Определение самоиндукции. Направление ЭДС самоиндукции
Замкнутый контур с током создает поток магнитной индукции (Ф) через поверхность S, которая ограничена этим контуром. Электродвижущая сила индукции ($\mathcal E$) появляется при любом изменении магнитного потока через поверхность (S), которую охватывает контур с током. Значит, если изменять силу тока в контуре, то в контуре появляется ЭДС. Такое явление называется явлением самоиндукции.
Направление вектора магнитной индукции поля, которое создает ток, определяется правилом правого винта, $\mathcal E$ в контуре связана с изменением потока правилом левого винта, значит, ЭДС самоиндукции направлена так, что препятствует изменению силы тока, которым она вызвана. Это правило называют правилом Ленца.
Индуктивность контура
Сила тока в контуре связывается с магнитным потоком с помощью выражения:
\[Ф=LI\ \left(1\right),\]где $L$ называют индуктивностью (коэффициентом самоиндукции) контура. Индуктивность контура равна магнитному потоку в процессе самоиндукции контура по которому течет ток силой в 1А.
Если среда не является ферромагнитной и контур не деформируется, ЭДС самоиндукции запишется как:
\[{{\mathcal E}}_{samInd}=-L\frac{dI}{dt}\left(2\right),\]где t -- время.
Линейная зависимость в формуле (1) между магнитным потоком и силой тока наблюдается если магнитная проницаемость среды ($\mu $) в которой находится контур не зависит от магнитной индукции ($\overrightarrow{B}$), то есть в отсутствии ферромагнетиков. Надо отметить, что форма уравнения (1) не изменится для любых веществ. Кроме того при постоянной силе тока поток вектора магнитной индукции изменяется с изменение формы и размеров контура.
Как уже отмечалось, L зависит от среды, в которой находится контур, его геометрических размеров и формы:
\[L=\frac{{\mu }_0}{4\pi }\int\limits_S{dS\oint\limits_l{\frac{\mu }{r^3}}}{\left[\overrightarrow{dl}\ \overrightarrow{r}\right]}_n\left(3\right),\]где $\mu $ -- относительная магнитная проницаемость среды, $\overrightarrow{r}$- радиус-вектор, который проводится от элемента контура с током ($\overrightarrow{dl}$) к элементу поверхности dS, поверхности S которая ограничена рассматриваемым контуром, индекс n означает проекцию на нормаль к dS. Для жесткого контура и в отсутствии ферромагнетиков L=const.
Основной единицей коэффициента самоиндукции в системе СИ является генри (Гн).
\[1Гн=1Вб/1А\ \left(4\right).\]Задание: Получите формулу, для вычисления коэффициента самоиндукции бесконечно длинного соленоида. Если даны n -- число витков соленоида на единицу длины, V- объем соленоида, $ \mu -\ $магнитная проницаемость среды.
Решение:
Если по соленоиду течет ток I, то внутри соленоида возникает однородное магнитное поле, индукция (В) которого равна:
\[B={\mu }_0\mu nI\ \left(1.1\right),\]где $n$ -- количество витков соленоида на единицу его длины ($n=\frac{N}{l}$), $N$ -- суммарное количество витков, $l$ -- длина соленоида.
В таком случае поток вектора магнитной индукции ($Ф'$) через любой виток соленоида равна:
\[Ф'=B\ \left(1.2\right),\]где $S$ -- площадь витка соленоида, она же площадь соленоида. Тогда полный поток (Ф) через все витки равен c учетом (1.1) и (1.2):
\[Ф=NФ=nlBS={\mu }_0\mu n^2I\ Sl\left(1.3\right).\]По определению коэффициент самоиндукции связан с магнитным потоком и силой тока выражением:
\[Ф=LI\left(1.4\right).\]Сравниваем формулы (1.3) и (1.4), получаем:
\[L={\mu }_0\mu n^2V\ ,\]где $V$ -- объем соленоида.
На практике индуктивность соленоида рассчитывают в соответствии с формулой:
\[L={k\mu }_0\mu n^2V\ ,\]где $k$ -- коэффициент который зависит от отношения длины соленоида ($l$) к диаметру его витков (d). Так при $l/d=0,1\ k=0,2;;\ при\ l/d=10\ k\approx 1.$Ответ: $L={\mu }_0\mu n^2V.$
Задание: Получите формулу, для вычисления коэффициента самоиндукции двухпроводной линии. Если даны R -- радиусы проводов, d- расстояние между проводами, $\mu =1-\ $магнитная проницаемость среды.
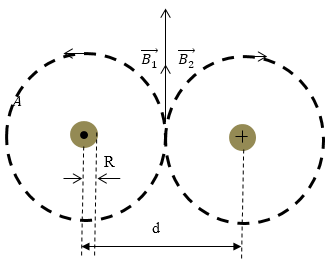
Рис. 1
Решение:
Двухпроводная цепь -- это два длинных параллельных проводника, которые входят в цепь тока. Токи в проводах направлены в противоположные стороны.
Найдем магнитный поток через площадь, которая ограничена осями проводов для отрезка длины l.
Рассмотрим один провод. Магнитное поле такого тока имеет осевую симметрию с центром на оси провода. Силовые линии поля при этом окружности с центрами на оси симметрии. По модулю значение магнитной индукции во всех точках силовой линии одинаково. Возьмем в качестве кривой циркуляции $A$ силовую линию радиуса r, тогда по теореме о циркуляции запишем:
\[\oint\limits_A{\overrightarrow{B}dr}=B\cdot 2\pi r\ (2.1)\]Для области внутри провода ($x \[B\cdot 2\pi r={\mu }_0\frac{I}{\pi R^2}\pi r^2={\mu }_0\frac{I}{R^2}r^2\to B=\frac{{\mu }_0I}{2\pi R^2}r\left(2.2\right).\]
Для области вне провода ($x\ge R$) магнитная индукция поля равна:
\[B\cdot 2\pi r={\mu }_0I\to B=\frac{{\mu }_0I}{2\pi r}\left(2.3\right).\]Соответственно поток ($Ф_{r\le R}$) через часть площади ($dS=lrdr$)внутри провода будет равен:
\[Ф_{r\le R}=\frac{{\mu }_0Il}{2\pi R^2}\int\limits^R_0{r}dr=\frac{{\mu }_0Il}{4\pi }\left(2.4\right).\]Поток ($Ф_{r\ge R}$) через остальную часть площади (при $r\ge R$) имеет вид:
\[Ф_{r\ge R}=\frac{{\mu }_0Il}{2\pi }\int\limits^d_R{\frac{dr}{r}=\frac{{\mu }_0Il}{2\pi }}ln\frac{R}{d}\left(2.5\right).\]Полный поток от одного провода можно найти как сумму потоков из выражений (2.4) и (2.5):
\[Ф=\frac{{\mu }_0Il}{4\pi }+\frac{{\mu }_0Il}{2\pi }ln\frac{R}{d}=\frac{{\mu }_0Il}{2\pi }\left(\frac{1}{2}+ln\frac{R}{d}\right)\left(2.6\right).\]Так как токи в проводах имеют противоположное направление, значит направления полей одинаковы. Поток от двух проводов в два раза больше, чем от одного. Значит:
\[Ф'=2Ф.\]Зная, что:
\[Ф'=IL\to L=\frac{Ф'}{I}\left(2.7\right),\]получим, что:
\[L=2\cdot \frac{{\mu }_0l}{2\pi }\left(\frac{1}{2}+ln\frac{R}{d}\right)=\frac{{\mu }_0l}{\pi }\left(\frac{1}{2}+ln\frac{R}{d}\right).\]Ответ: $L=\frac{{\mu }_0l}{\pi }\left(\frac{1}{2}+ln\frac{R}{d}\right).$












