Правила Кирхгофа для цепей переменного тока
Уравнение Ома для переменного тока:
\[I_mZ=U_m\ \left(1\right),\]где импеданс $Z=R+i\left(\omega L-\frac{1}{\omega C}\right)$ позволяет решать все задачи для переменного тока в цепи, которая содержит индуктивность, емкость, сопротивление. Роль этого закона такая же, как и закона Ома для цепей постоянного тока. Следовательно, схема анализа разветвленных цепей переменного тока аналогична, анализу цепей постоянного тока.
Представим, что имеем сложную цепь переменного тока. Мы должны рассматривать только квазистационарные токи, так как для их мгновенных значений справедливы законы Кирхгофа, что и для постоянных токов. Для любого замкнутого контура выполняется второе правило Кирхгофа:
где ${{\mathcal E}}_{mk}$ -- комплексные амплитуды ЭДС генераторов, $Z_k$ -- комплексные импедансы, $I_{mk}$ -- комплексные амплитуды сил тока.
[Определение] Для каждой точки разветвления цепи переменного тока выполняется первое правило Кирхгофа:
[/Определение]
Необходимо отметить, что законы постоянного тока применяются к комплексным амплитудам напряжения и ЭДС, тока и сопротивлений отдельных участков цепи. Получается, что любую задачу о расчете цепи переменного тока можно решить, если получить решение для схемы, по которой течет постоянный ток, а затем заменить все физические величины (токи, напряжения, ЭДС, сопротивления участков) на их комплексные аналоги.
Обобщение правил Кирхгофа на разветвленные цепи переменного тока было сделано Д.У. Рэлеем.
Как уже говорилось, каждая величина, которая входит в правила Кирхгофа является комплексной и уже содержит фазу (следовательно, и знак), при составлении уравнений надо проставлять знаки, так как один участок может принадлежать разным контурам, и соответственно может быть пройден по разным направлениям. Решение уравнений дает возможность найти как амплитуды всех сил токов, так и их фазы. Так как величины, входящие в уравнения комплексные, то количество уравнений в два раза больше, чем было бы, если бы токи были постоянными.
Метод контурных токов
При расчете сложных цепей используют метод контурных токов. Этот метод является следствием правил Кирхгофа. Сложный контур рассматривается как совокупность простых замкнутых контуров. В данном методе принимается то, что на всех участках каждого замкнутого контура течет один и тот же ток. Эти токи называются котурнами. Суммарная сила тока, которая течет по участку контура, равна алгебраической сумме сил контурных токов, для которых этот участок общий. Уравнение Кирхгофа записывается через контурные токи. При этом количество уравнений для контурных токов равно числу неизвестных токов.
Схема расчета сопротивления в цепи переменного тока
Для получения сопротивления цепи переменного тока можно применять простое правило. Гипотетически заменить каждую индуктивность ($L$) на комплексное сопротивление вида $i\omega L$, каждую емкость ($С$) - на $\frac{1}{i\omega C}$, все активные сопротивления оставить $R$. С полученными комплексными сопротивлениями провести те же операции, что и при вычислении сопротивления цепи постоянного тока, используя правила нахождения сопротивления параллельных и последовательных соединений. Полученная в результате комплексная величина $Z=X+iY$ будет комплексным сопротивлением цепи (импедансом). При этом $X$ -- активное сопротивление цепи, $Y$ -- реактивное сопротивление. Величина $\left|Z\right|$ -- модуль импеданса:
есть сопротивление цепи переменного тока, оно определяет амплитуду силы тока при известной амплитуде напряжения на концах цепи. Аргумент импеданса определяет угол ($\varphi $), на который напряжение опережает ток в цепи:
Описанный метод расчета комплексных сопротивлений часто применяется в электротехнике. Он не требует вычисления сдвигов фаз (что требуется при построении диаграмм), так как они учтены в комплексных сопротивлениях. Кроме того этот метод позволяет проводить вычисления с любой точностью, тогда как методы графический и векторных диаграмм наглядны, но не точны.
При последовательном соединении импедансов он рассчитывается как сумма:
При параллельном, соответственно:
Задание: Найдите токи, которые текут в участках цепи, которая изображена на рис.1. Считать известными импедансы, которые указаны на рисунке.
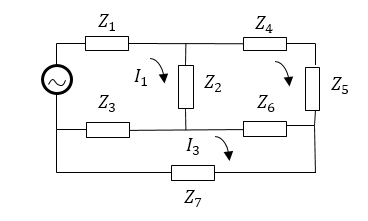
Рисунок 1.
Решение:
На рис.1 сложный контур состоит из трех простых контуров. В уравнении Кирхгофа при обходе замкнутого контура (между его узлами) используется сила тока, протекающая по этому участку. На каждом участке контура, в общем случае, сила тока отличается. Найдем полный импеданс для каждого участка контура между узлами (обозначим его соответствующим индексом). Положительное направление обхода обозначено стрелками.
Запишем уравнения, в соответствии с правилами Кирхгофа:
\[Z_{11}I_1+Z_{12}I_2+Z_{13}I_3=U\left(1.1\right),\] \[Z_{21}I_1+Z_{22}I_2+Z_{23}I_3=0\left(1.2\right),\] \[Z_{31}I_1+Z_{32}I_2+Z_{33}I_3=0(1.3).\]где $Z_{11},Z_{22},Z_{33}$ -- собственные импедансы контуров, равные:
\[Z_{11}=Z_1+Z_2+Z_3(1.4),\ \] \[Z_{22}=Z_4+Z_5+Z_6+Z_2\left(1.5\right),\] \[Z_{33}=Z_3+Z_6+Z_2\left(1.6\right).\]$Z_{12}$, $Z_{13}$... -- взаимные импедансы контуров. Они равны импедансам участков контуров, причем их знак зависит от того в каком направлении проходит ток соответствующий участок по отношению к контурному току. В нашем случае:
\[Z_{12}=-Z_2,\ Z_{21}=-Z_2\ \left(1.7\right).\]Количество уравнений, которые мы записали, равно количеству неизвестных токов. Решим нашу систему уравнений:
\[I_1=U\left(\frac{{\triangle }_{11}}{\triangle }\right),I_2=U\left(\frac{{\triangle }_{12}}{\triangle }\right),\ I_3=U\left(\frac{{\triangle }_{13}}{\triangle }\right)(1.8).\ \]где определитель системы равен:
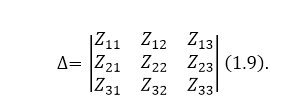
Рисунок 2.
${\triangle }_{11},{\triangle }_{12},{\triangle }_{13}$ -- дополнения элементов $Z_{11},Z_{12},Z_{13}$ в определителе $\triangle $:
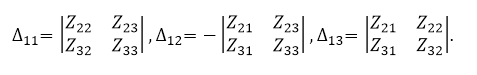
Рисунок 3.
Задача решена.
Задание: Цепь содержит конденсатор, емкость которого равна $C$, и активное сопротивление $R$ элементы соединены параллельно. Чему равен модуль импеданса? На какой угол напряжение опережает по фазе ток при таком соединении элементов?
Решение:
Заменим емкость $C$ на величину: $\frac{1}{i\omega C}$, учитывая, что соединение элементов параллельное, суммарный импеданс найдем как:
\[\frac{1}{Z}=i\omega C+\frac{1}{R}\to Z=\frac{1}{\frac{1}{R}+i\omega C}\left(2.1\right).\]Приведем выражение для импеданса к виду:
\[Z=X+iY\ \left(2.2\right).\]Для этого правую часть выражения (2.1) умножим и разделим на $\frac{1}{R}-i\omega C$, получим:
\[Z=\frac{\frac{1}{R}-i\omega C}{\frac{1}{R^2}+{\omega }^2C^2}=\frac{R-i\omega R^2C}{1+{\omega }^2C^2R^2}\left(2.1\right).\]Модуль импеданса равен:
\[\left|Z\right|=\sqrt{X^2+Y^2}=\frac{R}{\sqrt{1+{\omega }^2C^2R^2}}.\] \[\varphi =arctg\left(\frac{Y}{X}\right)=-arc\left(\omega RC\right).\]Ответ: $\left|Z\right|=\frac{R}{\sqrt{1+\omega^2C^2R^2}},\varphi=-arc\left(\omega RC\right).$











