В том случае, если обмотки генератора трехфазного тока соединить между собой специальным образом («звездой» или треугольником), то у такого тока возникают свойства, которые удобны в применении.
Векторная диаграмма напряжений для соединения «звезда»
Схема соединения звездой (рис.1(а)) и соответствующая векторная диаграмма напряжений на обмотках (рис.1(в)) изображены на рис.1. Здесь имеется точка $О$, которая называется точкой одинакового потенциала. Напряжение на каждой обмотке называется фазным (его амплитуда $U_{mf}$). Проводник, который соединен с точкой одинакового потенциала называют нулевым проводом. Проводники, которые соединены со свободными концами обмоток, называются фазными проводами. Получается, что фазные напряжения -- это напряжения между нулевым и фазными проводами. Напряжения между фазными проводами называют линейным (его амплитуда $U_{ml}$). Линейное напряжение между проводами 1-2 могут обозначать как $U_{12}$, между проводами 1-3 - $U_{13}$ и так далее.
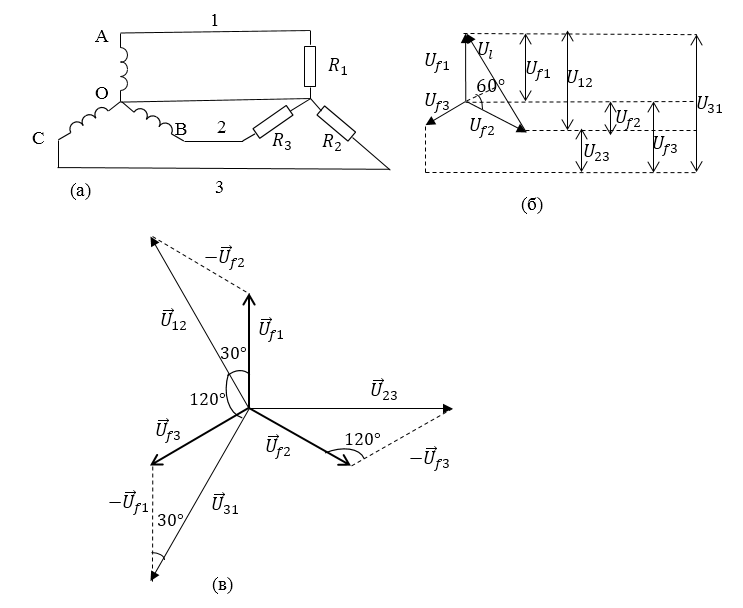
Рисунок 1.
Векторная диаграмма показывает, что амплитуды $U_{ml}\ $и $U_{mf}$находятся в соотношениях:
Ток, который течет через обмотки генератора называют фазным током ($I_f$), ток который течет в линиях называется током линии ($I_l$). В соединении звездой фазные токи равны токам в линии. Если сопротивления нагрузок не равны нулю, а $R_1=R_2=R_2=R$, то суммарная сила тока через нулевой провод равна нулю:
так как из векторной диаграммы видно, что $\sum\limits_i{U_i=0.}$
Векторная диаграмма напряжений для соединения «треугольник»
Схема соединения обмоток генератора треугольник изображена на рис.2. В этом случае амплитуды напряжений фазного и линейного равны ($U_{mf}=U_{ml}$).
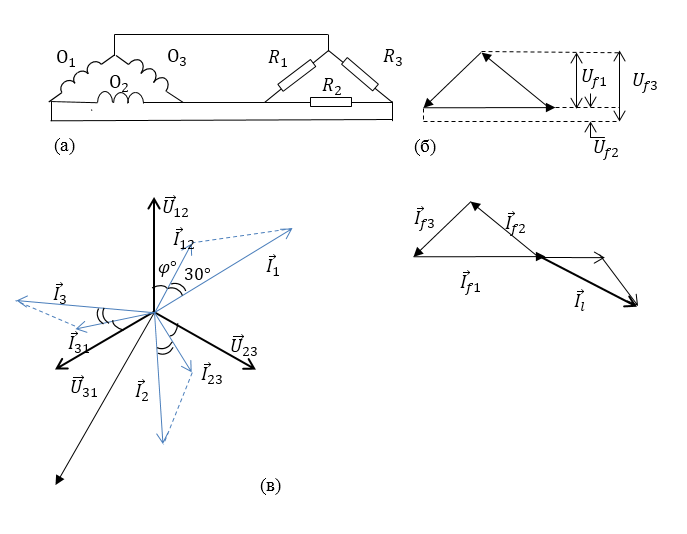
Рисунок 2.
Из векторной диаграммы токов (рис.2(в)) запишем амплитудных значений тока:
В соединении обмоток генератора треугольником ток замыкания в обмотках равен нулю. Однако это справедливо только для основной гармоники. Токи высших гармоник, появляющиеся из-за нелинейности колебаний, в обмотках есть.
Соединение нагрузок тоже может быть в виде звезды и в виде треугольника. На рис. 1 и рис.2 изображены соединения одного типа, как для генератора, так и для нагрузок. Но совсем не обязательно, что соединения обмоток генератора и нагрузок совпадают. Так, можно реализовать четыре возможные комбинации соединения генератора и нагрузок: «звезда» - «звезда», треугольник -- треугольник, «звезда» - треугольник, треугольник - «звезда». Каждое из перечисленных соединений имеет свои особенности.
Задание: В чем состоят особенности соединений «звезда» -- «звезда» и «звезда» - треугольник?
Решение:
- При соединении «звезда» -- «звезда» (рис.1) на всех нагрузках имеется разное напряжение. При одинаковых сопротивлениях ($R_1=R_2=R_3$) (или примерно равных) сила тока по нулевому проводу равна нулю (или очень мала). Теоретически нулевой провод можно убрать, но без него на каждую из пар нагрузок действует линейное напряжение, амплитудное значение которого равно:
Это напряжение распределяется между нагрузками в соответствии с величиной их сопротивлений. Такая зависимость напряжений от нагрузок крайне не удобна, поэтому нулевой провод сохраняют.
- При соединении «звезда» - треугольник (рис.3). На каждое сопротивление действует линейное напряжение равное:
Это линейное напряжение не зависит от величины сопротивления.
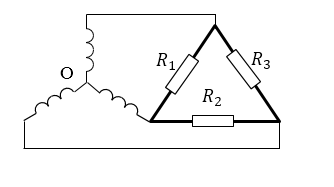
Рисунок 3.
Задание: Определите, чему равно фазное напряжение, если линейное $U_{ml}=220\ В$. Чему будет равно линейное напряжение, если 220 В считать фазным напряжением? Считать, что соединение обмоток генератора - «звезда».
Решение:
В том случае, если обмотки генератора соединены звездой, и это соединение имеет нулевой провод, в линии существует две системы напряжений (линейное и фазное), что является достоинством такого соединения.
Для соединения «звезда» мы имеем соотношение:
\[U_{ml}=\sqrt{3}U_{mf}\left(2.1\right).\]Следовательно, для фазного напряжение имеем:
\[U_{mf}=\frac{U_{ml}}{\sqrt{3}}=\frac{220}{\sqrt{3}}\approx 127\ \left(В\right).\]Если дано фазное напряжение, то:
\[U_{ml}=\sqrt{3}U_{mf}=\sqrt{3}\cdot 220\approx 380\ (В)\left(2.2\right).\]Ответ: 1. $U_{mf}=127\ В.$ $U_{ml}=380\ В.$











