Уравнение падающей, отраженной и преломленной волн, граничные условия
Поведение волны света на границе диэлектриков имеющих различную диэлектрическую проницаемость целиком определено граничными условиями для векторов волнового поля. В отсутствии свободных зарядов и током эти условия запишем как:
где индекс $\tau $ обозначает тангенциальную составляющую соответствующего вектора, индекс $n$ -- нормальную составляющую. Параметры падающей волны будем обозначать индексом ($pad$), отраженной ($otr$), преломленной ($pr$). Все параметры, относящиеся к среде, в которой распространяется падающая волна, будут иметь индекс $1$, к среде в которой распространяется преломленная волна -- индекс $2$. В таком случае напряженность электрического поля падающей волны запишем как:
напряженность электрического поля отраженной волны имеет вид:
для преломленной волны имеем:
при этом для волновых чисел имеем соотношения:
где $v_1=\frac{1}{\sqrt{\mu_1\mu_0\varepsilon_1\varepsilon_0}}$, $v_2=\frac{1}{\sqrt{{\mu }_2{\mu }_0{\varepsilon }_2{\varepsilon }_0}}$ -- скорости распространения волн в одной и второй средах. При этом вектор индукции магнитного поля перпендикулярен вектору напряженности электрического поля и совершает колебания в той же фазе (в диэлектрике).
Частоты полей волны при отражении и преломлении света
Если в граничное условие для тангенциальных составляющих электрического поля подставить выражения из правых частей формул (2), то мы имеем:
В выражении (4) начало радиус -- вектора выбирается произвольно. Его можно представить как:
где ${\overrightarrow{r}}_n$ -- нормальная составляющая радиус-вектора к поверхности раздела диэлектриков, ${\overrightarrow{r}}_{\tau }$ -- тангенциальная составляющая. Из равенства:
где ${\overrightarrow{k}}_n$ -- нормальная составляющая волнового вектора, ${\overrightarrow{k}}_{\tau }$ -- тангенциальная составляющая, сделаем вывод о том, что при переходе от одной точки поверхности к другой произведение ${\overrightarrow{k}}_n{\overrightarrow{r}}_n$ является постоянным, все изменения происходят за счет ${\overrightarrow{k}}_{\tau }{\overrightarrow{r}}_{\tau }.$ В связи с этим начало отсчета радиус- векторов берут в точке плоскости раздела сред. Для упрощения записи будем обозначать радиус -- вектор без индекса $\tau $, не смотря на то, что он лежит в плоскости раздела сред. Равенство (4) тождественно при произвольных и независимых изменениях t и $\overrightarrow{r}$ только в случае, если:
Мы показали, что частота световой волны при отражении и преломлении не изменяется.
Волновые векторы падающей, отраженной и преломленной волн
Волновой вектор $\overrightarrow{k}$ характеризует направление, которое принято называть лучом. Положим, начало отсчета вектора $\overrightarrow{r}$ в плоскости раздела сред, причем так, что $\overrightarrow{r}\bot {\overrightarrow{k}}_{pad}$, то есть можно записать, что:
В таком случае из выражения (8) следует, что:
Это означает, что векторы ${\overrightarrow{k}}_{ot}\bot \overrightarrow{r},{\overrightarrow{k}}_{pr}\bot \overrightarrow{r}$, следовательно, волновые векторы падающей, отраженной и преломленной волны лежат в одной плоскости.
Плоскость, в которой располагаются вектор падающей волны, нормаль к поверхности раздела в точке падения луча называют плоскостью падения луча.
Законы отражения и преломления света на границе двух диэлектриков
Допустим, что начало декартовой системы координат находится в точке падения луча. Ось $Z$ направлена в сторону среды распространения преломлённого луча. Плоскость $XZ$ пусть совпадает с плоскостью, в которой лежат падающий, отраженный и преломленный лучи (рис.1). Единичный вектор $\overrightarrow{n}$ -- нормаль к поверхности раздела веществ, он направлен во вторую среду. Единичный вектор $\overrightarrow{\tau }$ находится в плоскости раздела сред. Углы ${\alpha }_{pad},{\alpha }_{otr},\ {\alpha }_{pr}$ начинают отсчет от нормали к поверхности раздела сред, называют их соответственно, угол падения, отражения и преломления.

Рисунок 1.
Используя рис.1 запишем:
Используя выражение (8), получим:
Учтем равенства (3), имеем:
Из формулы (13) следует, что $sin\ {\alpha }_{pad}=sin\ {\alpha }_{otr}$, что означает:
Выражение (14) -- закон отражения: Угол падения равен углу падения. И из (13) имеем закон преломления Снеллиуса:
где $n_{12}$- показатель преломления второй среды относительно первой. Так как показатели преломления одной и второй сред относительно вакуума равны:
Задание: При каком угле падения отраженный луч перпендикулярен преломленному лучу, если известно, что граница раздела двух диалектиков плоская, показатель преломления второй среды относительно первой равен $n$.
Решение:
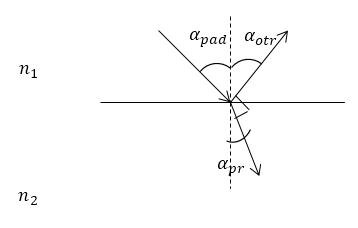
Рисунок 2.
В качестве основы для решения задачи примем закон преломления Снеллиуса:
\[\frac{sin\ \left({\alpha }_{pad}\right)}{sin\ \left({\alpha }_{pr}\right)}=n_{12}=n\left(1.1\right).\]и закон отражения:
\[{\alpha }_{pad}={\alpha }_{otr}\left(1.2\right).\]Из условия задачи и выражения (1.2) следует, что:
\[{\alpha }_{pr}=90{}^\circ -{\alpha }_{otr}\to sin\left({\alpha }_{pr}\right)={sin \left(90{}^\circ -{\alpha }_{otr}\right)\ }=cos\left({\alpha }_{otr}\right)\left(1.3\right).\]Подставим вместо $sin{\alpha }_{pr}$ в выражение (1.1) правую часть уравнения (1.3), учтем равенство углов падения и отражения, имеем:
\[\frac{sin\ \left({\alpha }_{pad}\right)}{sin\ \left({\alpha }_{pr}\right)}=\frac{sin\ \left({\alpha }_{pad}\right)}{cos\left({\alpha }_{pad}\right)}=tg\left({\alpha }_{pad}\right)=n\to {\alpha }_{pad}=arctg\left(n\right).\]Ответ: ${\alpha }_{pad}=arctg\left(n\right).$
Задание: Каким будет боковое смещение луча света ($x$), который проходит сквозь прозрачную пластинку, показатель преломления которой равен $n$, а ее толщина $d$. Свет падает пол углом $\alpha $.
Решение:
В задаче следует найти расстояние $ED=x$ (рис.3). Если считать, что первоначально свет распространялся в воздухе, то относительный показатель преломления вещества пластинки относительно воздуха равен $n$. Закон преломления запишем как:
\[\frac{sin\alpha }{{sin {\alpha }_{pr}\ }}=n\left(2.1\right).\]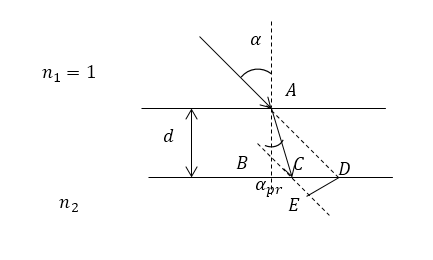
Рисунок 3.
Из рис.3 искомое расстояние ($ED=x$) равно:
\[ED=x=CDsin\left(90{}^\circ -\alpha \right)\left(2.2\right).\]Расстояние $CD$ найдем как:
\[CD=BD-BC\ \left(2.3\right),\]где
\[BD=\frac{d}{tg\left(90{}^\circ - \alpha\right)},\ BC=d\cdot tg\left(\alpha_{pr}\right)\left(2.4\right).\]Используя выражение (2.3), подставляем (2.4) в формулу (2.2), имеем:
\[x=\left(\frac{d}{tg\left(90{}^\circ -\alpha \right)}-d\cdot tg\left({\alpha }_{pr}\right)\right)sin\left(90{}^\circ -\alpha \right)=d\cdot sin\left(\alpha \right)\left(1-\frac{cos\left(\alpha \right)}{\sqrt{n^2-{sin}^2\alpha }}\right).\]Ответ: $x=d\cdot sin\left(\alpha \right)\left(1-\frac{cos\left(\alpha \right)}{\sqrt{n^2-{sin}^2\alpha }}\right).$












