Элементарная квантовая теория теплового излучения строится на основе двухуровневой модели атома. Допускают, что у атома имеется два дискретных энергетических состояния. Одно из них называют основным, его энергию обозначим $E_0$. Второе состояние именуется возбуждённым, его энергия $E_1.$ Количества атомов в каждом из данных состояний ($N_0\ и\ N_1$) называют населенностями уровней основного и возбужденного. Разность энергий описанных энергетических состояний равна энергии кванта света:
Данный квант поглощается в том случае, если переход осуществляется с нулевого на первый уровень и излучается, если переход осуществляется с первого на уровень $0$.
В соответствии с гипотезой Эйнштейна возможны следующие виды переходов между энергоуровнями:
-
Спонтанное излучение (рис.1). Атом первоначально находится в возбужденном состоянии $E_1$. В некоторый момент времени он самопроизвольно переходит в основное состояние. При этом атом испускает фотон. Данный процесс характеризуют вероятностью перехода в единицу времени.
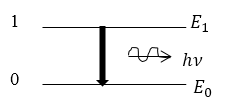
Рисунок 1. -
Поглощение (рис.2). В данном случае. Изначально атом находится в основном состоянии и, поглощая квант света, приходит в состояние возбуждения. Вероятность данного перехода пропорциональна плотности энергии электромагнитного поля на частоте перехода и некоторому коэффициенту, который зависит от вида атома. При каждом акте поглощения количество фотонов уменьшается на один.
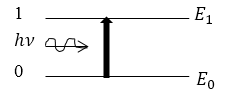
Рисунок 2.
Вышеназванные типы переходов соответствуют классической теории, но они не могут обеспечить сохранение энергетического баланса. Если вероятность спонтанного излучения зависит от внутренних свойств атома, то вероятность поглощения всегда определяется числом падающих фотонов имеющих определенную частоту. Значит, равновесие для всех частот не устанавливается. Для того чтобы устранить данное противоречие Эйнштейн предложил еще один тип перехода.
Вынужденное излучение (рис.3). Атом переходит из возбужденного состояния в основное под действием внешнего электромагнитного поля. Количество фотонов увеличивается на один. При вынужденном излучении новый фотон невозможно отличить от фотона, который вызвал переход. Все фотоны, которые появились в результате вынужденного излучения, имеют одинаковую частоту, фазу, направление распространения и поляризацию. Вынужденное излучение когерентно.
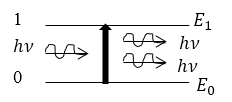
Рисунок 3.
Объектов с двумя энергетическими уровнями не существует в действительности. Существующие молекулы и атомы имеют существенно большее количество уровней энергии. Но, в условиях резонанса, если частота перехода между парой уровней в веществе близка к частоте света, обычно пренебрегают влиянием остальных уровней. В квантовой физике двухуровневая система играет важную роль, подобную роли гармонического осциллятора в классической физике. Данная модель используется в оптике для описания лазера и его взаимодействия веществом.
Коэффициенты Эйнштейна
Для равновесного состояния выполняется принцип детального равновесия. Согласно нему прямые и обратные процессы по каждому пути компенсируют друг друга. Используем принцип детального равновесия в применении к двум стационарным состояниям атома, которые будем характеризовать квантовыми числами n и m. Энергии данных квантовых состояний будем обозначать $E_n$ и $E_m$. Для определенности будем считать, что $E_n > E_m$. Прямыми и обратными процессами будем называть квантовые переходы атома между стационарными состояниями. С уровня $n$ на уровень $m$ будут возможны спонтанные и вынужденные переходы, а с уровня $m$ на уровень $n$ - только вынужденные. Пусть $A_{nm}$ -- отнесенная к единице времени вероятность того, что из состояния $n$ спонтанно переходит в состояние $m$, при этом излучается фотон энергии. Путь на уровне $n$ концентрация атомов равна $N_n$, то за единицу времени в единице объема на уровень $m$ перейдет спонтанно количество атомов равное:
Пусть $B_{nm}$ вероятность того, что атом под воздействием внешнего поля перейдет из состояния $n$ в состояние $m$, при этом излучается фотон энергии, причем данная вероятность отнесена к единице времени и единице спектральной плотности излучения. Количество атомов, которые перешли в единице объема за единицу времени с уровня n на уровень m равно:
Обозначим через $B_{mn}$ вероятность того, что атом вынужденно перейдет с уровня $m$ на уровень $n$, поглотив квант энергии, при чем, вероятность отнесена к единице времени и единице спектральной плотности излучения. За единицу времени в единице объема на уровень $n$ перейдет:
где $N_m$ -- концентрация атомов на уровне m, ${\nu }^B_{mn}$ -- количество атомов.
Параметры $A_{nm},\ B_{mn},\ B_{nm}$ -- коэффициенты Эйнштейна.
Условие равновесия между излучением и черным телом можно записать, используя коэффициенты Эйнштейна как:
Получите закон излучения черного тела на основании модели двухуровневой системы.
Решение:
В качестве основы для решения задачи используем представления о стационарных состояниях атомов, излучении атомов, как переходе из одного квантового состояния в иное и условие равновесия между черным телом и излучением в виде:
\[A_{nm}{exp \left(-\frac{E_n}{kT}\right)\ }+B_{nm}w_{\omega }{exp \left(-\frac{E_m}{kT}\right)=B_{mn}w_{\omega }{exp \left(-\frac{E_m}{kT}\right)\left(1.1\right).\ }\ }\]Если температура очень велика ($T\to \infty $), то спектральная плотность излучения $w_{\omega }\to \infty $. Разделим выражение (1.1) на $w_{\omega }\to \infty $, то получим:
\[B_{nm}={B_{mn} \left(1.2\right).\ }\]Выражение (1.2) означает, что вероятность вынужденного перехода с верхнего на нижний уровень равна вероятности вынужденного перехода с нижнего на верхний уровень. При этом из (1.1) получаем:
\[w_{\omega }=\frac{A_{nm}}{B_{nm}}\frac{1}{\left(exp\frac{\hbar \omega }{kT}\right)-1}\left(1.3\right).\]При малых частотах, когда $\frac{\hbar \omega }{kT}\ll 1$ имеем:
\[exp\frac{\hbar \omega }{kT}\approx 1+\frac{\hbar \omega }{kT}\left(1.4\right).\]Формула (1.3) принимает вид:
\[w_{\omega }=\frac{A_{nm}}{B_{nm}}\frac{kT}{\hbar \omega }\left(1.5\right).\]Сравним выражение (1.5) с формулой Рэлея -- Джинса:
\[w\left(\omega ,T\right)=\frac{\omega^2}{{\pi}^2c^3}kT\left(1.6\right).\]Получим, что:
\[\frac{A_{nm}}{B_{nm}}=\frac{{\hbar \omega}^3}{{\pi}^2c^3}\left(1.7\right).\]Подставим вместо найденного соотношения $\frac{A_{nm}}{B_{nm}}$ правую часть выражения (1.7) в формулу (1.3), имеем:
\[w_{\omega }=\frac{{\hbar \omega }^3}{{\pi }^2c^3}\frac{1}{\left(exp\frac{\hbar \omega }{kT}\right)-1}.\]Так, мы получили формулу Планка для излучения абсолютно черного тела.
Когда возможны вынужденные и спонтанные переходы атомов?
Решение:
С низкого энергетического уровня на более высокий энергетический уровень электрон может перейти, только поглотив фотон, то есть вынужденно. Спонтанно перейти на более высокий уровень атом не может, так как это вступает в противоречие с законом сохранения энергии.
Переходы атомов с более высоких уровней на более низкие энергетические уровни возможны: вынужденные (вызванные внешними к атому причинами) и самопроизвольные (вызванные внутренними причинами).











