Энергетическая светимость ($R$) определяется как мощность излучения ($dP$) с элемента поверхности по всем направлениям:
Стефан предложил следующую связь между температурой тела и энергетической светимостью:
где $\varepsilon \le 1$ -- коэффициент излучения (коэффициент черноты), $T$ -- термодинамическая температура, $\sigma =5,67\cdot {10}^{-8}\frac{Вт}{м^2К^4}$ -- постоянная Стефана -- Больцмана.
Излучение, которое падает на поверхность тела, поглощается частично. Отношение поглощенной энергии к падающей - коэффициент поглощения ($\alpha \le 1$). Для светлых тел $\alpha $ -- малая величина.
Тела, которые поглощают всю падающую на них энергию, называют черными ($\alpha =1$). Излучательную способность абсолютно черного тела обозначим $R_e$. При взаимодействии вещества и излучения особенно интересным является вопрос о термодинамическом равновесии. В термодинамическом равновесии температура тела неизменна, что означает, за единицу времени тело поглощает и испускает одинаковую энергию теплового излучения.
На основе представлений термодинамики Кирхгоф показал, что $\varepsilon =\alpha $, для любой температуры и для каждой длины волны в отдельности. Получается, что для абсолютно черного тела $\varepsilon =1.$ Это означает, что черное тело - самый эффективный излучатель тепловой радиации.
В экспериментах, тепловое излучение черного тела реализуется как излучение маленького отверстия в большой полости (рис.1). Излучение попадало в полость и много раз отражается от внутренней поверхности и соответственно поглощается на ее внутренних стенках и почти не излучалось из полости. Если стенки полости поддерживать при некоторой постоянной температуре, то из отверстия выходит излучение очень близкое по спектру к излучению абсолютно черного тела. Значит, поверхность отверстия ведет себя как абсолютно черное тело. Излучение, которое выходит из отверстия является равновесным тепловым излучением.
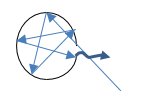
Рисунок 1.
При теоретических исследованиях для описания спектрального состава равновесного излучения используют функцию частоты ($f\left(\omega ,T\right)=\frac{с}{4}w_{\omega }\left(\omega ,T\right)$). В эмпирических работах чаще пользуются функцией длины волны ($\varphi (\lambda ,T)$).
Данные функции связаны между собой соотношениями:
Раскладывая спектр излучения, используя дифракционную решетку, проводя измерения разных участков спектра, строят функции $\varphi \left(\lambda ,T\right)\ и\ f\left(\omega ,T\right).$ Площадь, которую охватывает кривая, при этом равна энергетической светимости абсолютно черного тела при соответствующей температуре.
Законы, характеризующие излучение абсолютно черного тела
Закон Стефана - Больцмана показывает, что мощность излучения поверхности абсолютно черного тела зависит только от температуры и не связана с физическими свойствами поверхности объекта:
Стефан исследовал излучение черного тела эмпирически, а Больцман получил выражение (3) теоретически, поэтому закон называют законом Стефана -- Больцмана.
Энергия при равновесном тепловом излучении распределена по длине волны. Теоретически данный вопрос изучал В. Вин. Он показал, что в плотности распределения энергии теплового излучения по длинам волн присутствует максимум, который относится к длине волны (${\lambda }_{max}$), которая определена соотношением:
Соотношение (4) называют законом смещения Вина. Эмпирически показано, что данный закон хорошо выполняется.
Надо отметить, что попытки описать весь спектр излучения черного тела основываясь на теории классической физики, потерпели неудачу. В $1900$ г. М. Планк создал интерполяционную формулу, которая согласуется с экспериментом и полностью описывает особенности излучения абсолютно черного тела:
где $\hbar =1,05\cdot {10}^{-34}Дж\cdot с$, $w_{\omega }$ --спектральная плотность энергии излучения.
При $\hbar \omega \ll kT$ формула Планка переходит формулу Рэлея - Джинса:
Данная формула определяет распределение теплового излучения по спектру. Она хорошо согласуется с опытами при малых частотах.
При $\hbar \omega \gg kT$ формула Планка переходит в формулу Вина:
Выражение (7) подтверждают эксперименты, которые проводят в области больших частот.
Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощательную способность близкую к единице только в ограниченном интервале частот. Так в инфракрасной области их поглощательная способность существенно меньше единицы.
Теория излучения для абсолютно черного тела имела большое значение в физике, так как она привела к введению понятия кванта энергии.
На рис. 2 заданы графики функции $\varphi \left(\lambda ,T\right)$ при разных температурах ($T_1и\ T_2$), для какого из графиков больше температура тела выше? Что происходит с максимумом испускательной способности данного тела при росте температуры?
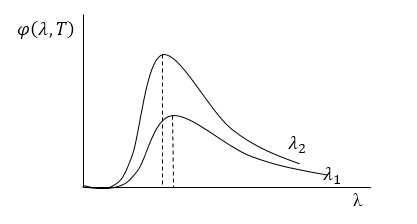
Рисунок 2.
Решение:
Так как мы знаем, что площадь, которую охватывает кривая заданная функцией $\varphi \left(\lambda ,T\right)$, равна энергетической светимости абсолютно черного тела при соответствующей температуре, то из графиков, очевидно, что площадь, соответствующая$\ {\lambda }_1$ меньше, чем при ${\lambda }_2$. Получаем, что $T_1
Максимум испускательной способности при увеличении температуры перемещается в сторону коротких длин волн (больших частот).
Ответ: $T_1
Какую массу теряет Солнце при излучении, за время t, если считать его абсолютно черным телом? Максимальная спектральная плотность энергетической светимости Солнца соответствует ${\lambda }_0.$
Решение:
Используем закон Вина для нахождения температуры Солнца:
\[{\lambda }_{max}T=b\to T=\frac{b}{{\lambda }_0}\left(2.1\right).\]Энергия, которую излучает Солнце за время t, равна:
\[W=R_eSt\ \left(2.2\right),\]где $S=4\pi R^2$ -- площадь поверхности Солнца, R- радиус Солнца. Величину $R_e$ найдем из закона Стефана - Больцмана:
\[R_e=\sigma T^4\left(2.3\right).\]Подставим выражение для $R_e$ в формулу (2.2), имеем
\[W=\sigma T^44\pi R^2t\ \left(2.4\right).\]Изменение массы Солнца найдем в соответствии с формулой:
\[\triangle m=\frac{W}{c^2}=\frac{\sigma T^44\pi R^2t\ }{c^2}=\frac{\sigma 4\pi R^2t\ }{c^2}{(\frac{b}{{\lambda }_0})}^4.\]Ответ: $\triangle m=\frac{у4\pi R^2t\ }{c^2}{(\frac{b}{\lambda_0})}^4.$











