Закон распределения молекул по скоростям
Закон распределения молекул по скоростям описывает распределение частиц макроскопической системы при условии, что эта система находится в состоянии термодинамического равновесия, распределение является стационарным и внешние силы на систему не действуют. Данное распределение выполняется как для газов, так и жидкостей, если в них можно использовать законы классической механики.
Определить, каким образом распределены молекулы по скоростям, -- это значит ответить на вопрос: «сколько молекул имеет ту или иную скорость при заданной температуре в состоянии равновесия?» Для разъяснения вопроса введем понятие: «пространство скоростей» (рис.1). В таком пространстве на декартовых осях отложены не координаты, а проекции скоростей.
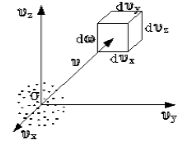
Рис. 1
В таком случае поставленный вопрос изменится на вопрос о том, как распределены молекулы в пространстве скоростей. Понятно, что молекулы распределены неравномерно.
Если в пространстве скоростей выделить параллелепипед объема $dw=dv_xdv_ydv_z$, тогда количество молекул, которые попадут в него $dN_v.$ Предположим, что N- количество молекул газа, $f(v)$- некоторая функция скорости. Тогда
Распределение Максвелла
Как было отмечено, газ находится в состоянии равновесия, все направления движения частиц равноправны, следовательно, распределение молекул в пространстве скоростей можно считать сферически симметричным (рис.2).
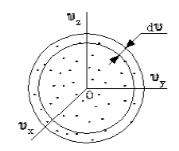
Рис. 2
Найдем число молекул в шаровом слое $dv$:
Разделим (2) на число частиц (N) и найдем вероятность$\ (dW_v)$ того, что модуль скорости молекулы находится в пределах от $v\ до\ v+dv$:
где $F\left(v\right)$- функция распределения вероятности значения $v.\ $Эту функцию теоретически получил Д. Максвелл.
Таким образом, распределение молекул по скоростям (вернее их модулям) запишем как:
\[dN_v=N4\pi {\left(\frac{m_0}{2\pi kT}\right)}^{\frac{3}{2}}exp\left(-\frac{m_0v^2}{2kT}\right)v^2dv\ \left(5\right),\]при этом $v=\sqrt{{v_x}^2+{v_y}^2+{v_z}^2}$, $m_0$- масса молекулы, k -- постоянная Больцмана.
Можно записать распределение Максвелла по проекциям скоростей:
\[dN=Nf\left(v_x\right)f\left(v_y\right)f\left(v_z\right)dv_xdv_ydv_{z\ }\left(6\right),\]при этом
\[f\left(v_i\right)={\left(\frac{m_0}{2\pi kT}\right)}^{\frac{1}{2}}exp\left(-\frac{m_0{v_i}^2}{2kT}\right)\ \left(i=x,y,z\right)\left(7\right),\]где $v_x,v_y,v_{z\ }$ - проекции скорости молекулы на оси координат.
Еще один из вариантов написания распределения Максвелла по модулям скоростей представлен в виде:
\[dN=N\frac{4}{\sqrt{\pi }{v_{ver}}^3}{exp \left(-{\left[\frac{v}{v_{ver}}\right]}^2v^2\right)\ }dv\left(8\right),\]где $v_{ver}$ -- вероятнейшая скорость молекулы.
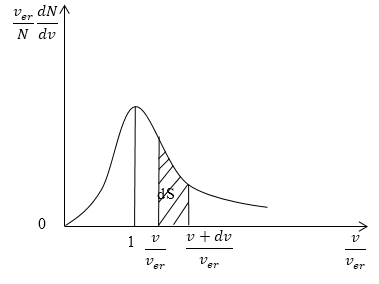
Рис. 3
На рисунке 3 изображена кривая закона распределения молекул по скоростям. Доля молекул газа, скорости которых лежат в интервале от $v\ до\ v+dv,$ пропорциональна заштрихованной площади dS под кривой.
Поскольку скорости всех молекул лежат в интервале от $0\ до+\infty $, то выполняется равенство:
\[\int\nolimits^{\infty }_0{f\left(v\right)dv}=1\ \left(9\right).\]Это так называемое условие нормировки функции распределения.
Таким образом, распределение Максвелла зависит от массы молекулы газа и его температуры. Давление и объем в распределение не входят.
Задание: Используя распределение Максвелла, найдите наиболее вероятную скорость молекул газа в равновесном состоянии газа при температуре T.
Решение:
За основу возьмем распределение молекул по модулям скоростей:
\[dN_v=N4\pi {\left(\frac{m_0}{2\pi kT}\right)}^{\frac{3}{2}}exp\left(-\frac{m_0v^2}{2kT}\right)v^2dv\ \left(1.1\right).\]Наиболее вероятной скорости соответствует максимум функции, то продифференцируем выражение (1.1) по скорости и приравняем к нулю, получим:
\[\frac{dN_v}{dv}=N4\pi {\left(\frac{m_0}{2\pi kT}\right)}^{\frac{3}{2}}\left[2v_{ver}exp\left(-\frac{m_0{v_{ver}}^2}{2kT}\right)-{v_{ver}}^2\frac{m_02v_{ver}}{2kT}exp\left(-\frac{m_0{v_{ver}}^2}{2kT}\right)\right]=0\to \] \[2v_{ver}-{v_{ver}}^2\frac{m_02v_{ver}}{2kT}=0\to 1-{v_{ver}}^2\frac{m_0}{2kT}=0\to {v_{ver}}^2=\frac{2kT}{m_0}\] \[v_{ver}=\sqrt{\frac{2kT}{m_0}}\ (1.2)\]Ответ: Наиболее вероятная скорость молекул газа $v_{ver}=\sqrt{\frac{2kT}{m_0}}.$
Задание: Пусть $Т_1
Решение:
Из формулы для наиболее вероятной скорости молекул газа, полученной в предыдущем примере:
\[v_{ver}=\sqrt{\frac{2kT}{m_0}}\ (2.1)\]очевидно, что с увеличением температуры скорость растет, то есть максимум кривой смещается в сторону больших скоростей. Площадь под кривой распределения величина постоянная, следовательно, кривые изобразим следующим образом (рис.4).
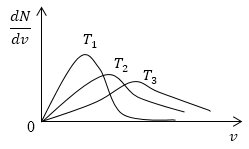
Рис. 4
Задание: На рис. 5 представлен график функции распределения молекул по проекциям скорости $v_x$. Сравнить числа молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$и от $v_{x1}$ до $v_{x2}$.
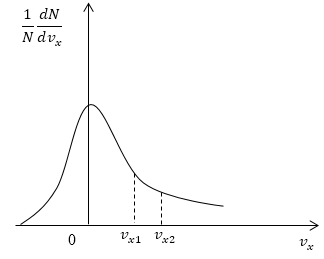
Рис. 5
Решение:
Как уже отмечалось в теоретической части, доля молекул газа, скорости которых лежат в интервале от $0\ до\ v_{x1},$ пропорциональна площади $S_1$ фигуры, которая ограничена кривой распределения, вертикальной осью (0$\ \frac{1}{N}\frac{dN}{dv_x})$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей проходящей через точку $v_{x1}$. Во втором случае доля молекул газа, скорости которых лежат в интервале от $v_{x1}\ до\ v_{x2},$ пропорциональна площади $S_2$ фигуры, которая ограничена кривой распределения, вертикальной прямой параллельной оси (0$\ \frac{1}{N}\frac{dN}{dv_x}),\ проходящей\ через\ точку\ v_{x1}$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей, проходящей через точку $v_{x2}$. Очевидно, что $S_1>S_2.\ $ Следовательно, молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.
Ответ: Молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.











