Что такое температура
Температура -- скалярная физическая величина, характеризует состояние термодинамического равновесия макроскопической системы тел.
Температурой также называют физическую величину, характеризующую степень нагретости тела, но этого для понимания смысла и значения понятия температура не достаточно. В этой фразе наблюдается лишь замена одного термина другим и не более понятным. Обычно физические понятия связаны с какими-то фундаментальными законами и получают смысл только в связи с этими законами. Понятие температура связано с понятием теплового равновесия и, следовательно, с законом макроскопической необратимости.
Изменение температуры
В состоянии термодинамического равновесия все тела, образующие систему, имеют одинаковую температуру. Измерение температуры можно произвести только косвенным путем, основываясь на зависимости от температуры таких физических свойств тел, которые можно измерить непосредственно. Применяемые для этого вещества (тела) называют термометрическими.
Пусть два теплоизолированных тела приведены в тепловой контакт. От одного тела к другому устремится поток энергии, будет происходить процесс теплопередачи. При этом считается, что тело, которое отдает тепло имеет большую температуру, чем тело к которому поток тепла устремился. Естественно, что через некоторое время поток энергии прекращается, наступает тепловое равновесие. Предполагается, что температуры тел выравниваются и устанавливается где-то в интервале между исходными значениями температур. Так, получается, что температура -- некоторая метка теплового равновесия. Получается, что любая величина t, которая удовлетворяет требованиям:
- $t_1>t_2$, если поток тепла идет о первого тела ко второму;
- $t'_1=t'_2=t,\ t_1 > t > t_2$, при установлении теплового равновесия может быть принята за температуру.
При этом предполагается, что тепловое равновесие тел подчиняется закону транзитивности: если два тела находятся в равновесии с третьим, то они находятся в тепловом равновесии и между собой.
Важнейшей особенностью приведённого определение температуры является его неоднозначность. Мы по-разному можем выбрать величины, удовлетворяющие поставленным требованиям (что отразится в способах измерения температуры), и получить несовпадающие температурные шкалы. Температурные шкалы -- это способы деления на части интервалов температур.
Приведем примеры. Как известно, прибор для измерения температуры -- термометр. Рассмотрим два типа термометров различного устройства. В одном роль температуры тела выполняет длина ртутного столбика в капилляре термометра, в случае когда термометр находится в тепловом равновесии с телом, температуру которого мы измеряем. Длина ртутного столбика удовлетворяет условиям 1 и 2, которые приведены выше и предъявляются к температуре.
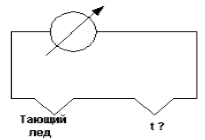
рис. 1
Существует и другой способ измерения температуры: с помощью термопары. Термопарой называют электрическую цепь с гальванометром и двумя спаями разнородных металлов (рис. 1). Один спай помещен в среду с фиксированной температурой, например тающий лед, другой в среду, температуру которой надо определить. В этом случае температурным признаком считают ЭДС термопары. Эти два способа измерения температуры не будут давать одинаковых результатов. И для того, чтобы перейти от одной температуре к другой, необходимо построить градировочную кривую, устанавливающую зависимость ЭДС термопары от длины ртутного столбика. Тогда равномерная шкала ртутного термометра преобразуется в неравномерную шкалу термопары (или наоборот). Равномерные шкалы ртутного термометра и термопары образуют две совершенно разные температурные шкалы, на которых тело в одном и том же состоянии будет иметь различные температуры. Можно взять одинаковые по устройству термометры, но с различными "термическими телами" (например, ртутью и спиртом). Их температурные шкалы также не совпадут. График зависимости длины ртутного столбика от длины спиртового столбика не будут линейными.
Отсюда следует, что понятие температуры, основанное на законах теплового равновесия, не однозначно. Такая температура называется эмпирической, она зависит от способа измерения температуры. Нуль шкалы эмпирической температуры всегда выбивается произвольно. По определению эмпирической температуры физический смысл имеет только разность температур, то есть ее изменение. Любая эмпирическая температурная шкала приводится к термодинамической температурной шкале введением поправок, учитывающих характер связи термометрического свойства с термодинамической температурой.
Температурные шкалы
Для построения шкалы температур приписывают численные значения температуры двум фиксированным реперным точкам. За тем делят разность температур реперных точек на выбранное произвольным образом число частей, получая единицу измерения температуры. В качестве исходных значений, служащих при построении шкалы температуры для установления начала отсчета и ее единицы -- градуса, применяют температуры перехода химически чистых веществ из одного агрегатного состояния в другое, например температуру плавления льда $t_0$ и кипения воды $t_k$ при нормальном атмосферном давлении ($\approx 10^5Па).$ Величины $t_0\ и\ t_k$ имеют разные значения:
- по шкале Цельсия (стоградусной шкале): температура кипения воды $t_k=100^0C$, температура плавления льда $t_0=0^0С$. Шкала Цельсия -- это такая шкала в которой температуры тройной точки воды 0,010С при давлении 0,06 атм. (Тройной точкой воды называют определенную температуру и давление, при которых могут существовать в равновесии одновременно вода, ее пар и лед.);
- по шкале Фаренгейта температура кипения воды $t_k=212^0F;$ $t_0$=3$2^0F$ -- точка таянья льда;
- по шкале Кельвина: температуру отсчитывают от абсолютного нуля (t=-273,50C) и называют термодинамической или абсолютной температурой. T=0K -- это состояние, соответствующее полному отсутствию тепловых колебаний. Температура кипения воды по этой шкале $t_k=373К,$ температура плавления льда $t_0=273К$. Связь между температурой по кельвину и температурой по Цельсию: \[T\left(K\right)=t^0C+273,15^0C\left(2\right);\]
- по шкале Реомюра температура кипения воды $t_k=80^0R$, температурa плавления льда $t_0=0^0R.$ Шкала практически вышла из употребления. Связь между температурами, выраженными в градусах Цельсия и градусом Реомюра: \[1^0С=0,8^0R\left(3\right);\]
- по шкале Ранкина точка кипения воды $t_k=671,67^{0\ }Ra$, температурa плавления льда $t_0={491,67}^0Ra.$ Начинается шкала от абсолютного нуля. Число градусов между точками замерзания и кипения воды по шкале Фаренгейта и Ранкина одинаково и равно 180.
Связь между температурами, выраженными в градусах Цельсия и Фаренгейта, имеет вид:
\[\frac{t^0C}{100}=\frac{t^0F-32}{180}\ \ или\ t^0F=1,8t^0C+32\ \left(1\right);\]Ноль на этой шкале определяется по температуре замерзания смеси воды, соли и нашатыря в пропорции 1:1:1.
В термометре Реомюра использовался спирт.
Соотношение между кельвином и градусом Ранкина: 1К=1,$8^{0\ }Ra$, градусы Фаренгейта переводятся в градусы Ранкина по формуле:
\[^0Ra=^0F+459,67\left(4\right);\]В технике и в быту используется температура по шкале Цельсия. Единица этой шкалы называется градусом Цельсия ($^0С).\ $ В физике пользуются термодинамической температурой, которая не только более удобна, но и имеет глубокий физический смысл, так как определяется средней кинетической энергией молекулы. Единица термодинамической температуры -- градус кельвина (до 1968 г.), или сейчас просто кельвин (К), является одной из основных единиц в СИ. Температура T=0К называется абсолютным нулем температуры. Современная термометрия основана на шкале идеального газа, где в качестве термометрической величины используют давление. Шкала газового термометра абсолютна (T=0, p=0). При решении задач чаще всего вам придется использовать именно эту шкалу температур.
Задание: Считается, что температура комфорта в помещении равна от $+18^oС$ до $+22^oС$. Рассчитайте, каковы границы интервала температурного комфорта по термодинамической шкале.
Решение:
Используем соотношение:
\[T\left(K\right)=t^0C+273,15^0C\]Тогда значение температуры нижней границы комфорта:
\[T=18+273\approx 291\ \left(K\right),\]значение температуры верхней границы комфорта:
\[T=22+273\approx 295\ (К)\]Ответ: Границы интервала температурного комфорта по термодинамической шкале от 291 К до 295 К.
Задание: Определите, при какой температуре показания термометров по шкалам Цельсия и Фаренгейта одинаковы?
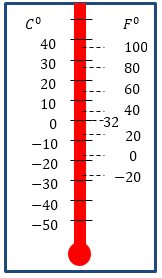
рис. 2
Решение:
Используем соотношение:
\[t^0F=1,8t^0C+32\ \left(2.1\right).\]Если температуры равны, то можем записать выражение (2.1) в следующем виде:
\[x=1,8x+32\ \left(2.2\right).\]Найдем x:
\[x=-\frac{32}{0,8}=-40\ (^0C)\]Ответ: При $-40^oС$ (или $-40^oF$) показания термометров по шкалам Цельсия и Фаренгейта одинаковы.











