
Неравномерно нагретый проводник (полупроводник) ведет себя как система физически разных проводников (полупроводников), которые находятся в контакте. Томсон пришел к заключению и подтвердил это эмпирически, что на границах таких участков происходит выделение (поглощение) теплоты Пельтье. Такое явление было названо явлением Томсона, а теплота, которая выделяется на границах этих участков, называется теплотой Томсона. Эффект Томсона объясняется изменением свойств проводников при нагревании. Первоначально однородный проводник при неравномерном нагреве превращается в неоднородный. Значит, явление Томсона, по своей сути, является эффектом Пельтье. Только неоднородность в данном случае вызывается не химическим различием состава вещества, а градиентом температуры.
Сущность явления Томсона с точки зрения классической теории
Классическая электронная теория проводимости явление Томсона объясняет довольно просто. Допустим, что у нас имеется полупроводник с электронной проводимостью. Градиент температуры направлен от точки 2 к точке 1 ($T_1>T_2$). Вследствие диффузии концентрация электронов в точке 1 становится меньше, чем в точке 2. Так, возникнет электрическое поле ($\overrightarrow{E}$), которое направлено от точки 1 к точке 2 (против направления $grad(T)$). Если вдоль проводника течет ток, в направлении $grad(T)$, то поле будет замедлять электроны, температура участок 1 2 станет уменьшаться. Если ток течет в обратном направлении, то участок проводника 1 2 будет нагреваться. В дырочном проводнике ситуация будет обратной. Ситуация представится так, как будто на обычный поток тепла, который вызывается теплопроводностью, накладывается дополнительный поток теплоты, который связан с течением тока. В дырочных полупроводниках дополнительный поток теплоты имеет направление такое же, как направление тока. В электронных полупроводниках направления тока и теплоты потока тепла противоположны.
Эффект Томсона считают положительным, если ток, который течет в направлении градиента температуры вызывает повышение температуры вещества.
Дифференциальная и интегральная формы уравнения для эффекта Томсона
Допустим, что $Q_T$- тепло Томсона, которое выделятся за время t в объеме проводника равном $V$. В таком случае количество теплоты, которое выделяется в единице объема на единицу времени ($\frac{Q_T}{Vt}$) может быть представлено как:
где$\ \sigma $ -- коэффициент Томсона. Этот коэффициент зависит от вещества, его состояния, например от температуры. Выражение (1) называют дифференциальной формой уравнения, которое описывает явление Томсона.
Рассмотрим проводник длиной $\triangle x$, и сечением $S$. Концы этого проводника имеют маленькую разность температур $\triangle T$. Так как $\triangle T$ считаем небольшой, то мы в праве не учитывать зависимость $\sigma $ от температуры. Можно записать, что объем проводника равен:
Полная сила тока ($I$) равна:
где $j$ -- плотность силы тока, а
Тогда выражение (1) можно записать как:
Формула $Q_T=\sigma \triangle TIt$ представляет собой интегральную форму уравнения, которое описывает явление Томсона. Она дает полное количество теплоты Томсона, которое выделяется во всем рассматриваемом отрезке проводника.
Тепло $Q_T>0$, если оно выделяется. Положительным направлением тока принимают направление от холодного к горячему (направление градиента температур).
Величина коэффициента Томсона очень небольшая. Так для висмута она равна примерно $\sigma \sim {10}^{-5}\frac{В}{К}$.
Явление Томсона возникает потому, что в проводнике с током существует поток энергии, которая пропорциональна плотности тока. При существовании градиента температур в проводнике присутствует еще поток энергии, вызванный теплопроводностью, однако он от тока не зависит, его часто не учитывают.
Задание: Получите, выражение для энергии Томсона, исходя из потоков энергии, которая возникает при градиенте температур в проводнике. Поток энергии, который вызван теплопроводностью, можно не учитывать.
Решение:
Рассмотрим в однородном проводнике очень тонкий слой, ограниченный плоскостями $x=const\ и\ x+dx=const\ $единичной площади. Тогда его объем равен $dx$. Пусть электроны перемещаются вдоль оси X. Температуры на выбранных плоскостях равны $Tи\ T+dT$, потоки энергии через эти плоскости равны $Pи\ P+dP.$ Значит, в каждый момент времени в объем будет входить энергия равная $P$ и выходить - энергия $P+dP.$ Тогда, в единице энергии объема будет выделяться энергия, равная:
\[\frac{Q_T}{Vt}=\frac{P\left(x\right)-P(x+dx)}{dx}=-\frac{dP\left(x\right)}{dx}\ \left(1.1\right).\]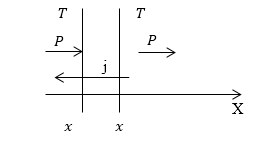
Рисунок 1.
Если $\left\langle E_k\right\rangle -\ $средняя кинетическая энергия для N электронов, потенциальная энергия электрона равна ${-q}_e\varphi $, тогда поток энергии равен:
\[P=-\frac{j}{q_e}\left(\left\langle E_k\right\rangle {-q}_e\varphi \right)\left(1.2\right).\]Подставим выражение (1.2) вместо $P$ в формулу (1.1), получим:
\[\frac{Q_T}{Vt}=\frac{j}{q_e}\frac{d\left\langle E_k\right\rangle }{dx}-j\frac{dц}{dx}\ \left(1.3\right),\]где $-\frac{d\varphi }{dx}=E$ -- напряженность электрического поля. Можно записать, следующее:
\[\frac{d\left\langle E_k\right\rangle }{dx}=\frac{d\left\langle E_k\right\rangle }{dT}\frac{dT}{dx}\left(1.4\right).\]Из (1.3), применяя (1.4) запишем:
\[\frac{Q_T}{Vt}=\frac{j}{q_e}\frac{d\left\langle E_k\right\rangle }{dT}\frac{dT}{dx}-jE\ \left(1.5\right),\]где $jE$ -- тепло Джоуля -- Ленца в единице объема и в единицу времени. Первое слагаемое в выражении (1.5) есть тепло Томсона так же в единице объема и единицу времени.
Ответ: $\frac{Q_T}{Vt}=\frac{j}{q_e}\frac{d\left\langle E_k\right\rangle }{dT}\frac{dT}{dx}$.
Задание: Клаузиус применил к явлениям термоэлектричества принципы термодинамики. Он рассматривал термопару, горячий спай ее поддерживался при температуре $T_1$, холодный при температуре $T_2$. Он считал, что при прохождении тока I в спае 1 за 1 с выделяется теплота Пельтье, в спае 2 поглощается теплота Пельтье, выделяется джоулево тепло. Вычислял термоэлектродвижущую силу, получал результат, который не согласовывался с экспериментом. Объясните почему? Считайте, что разность температур $T_1-T_2\to 0.$ Чему равен коэффициент термоэлектродвижущей силы?
Решение:
Проблема Клаузиуса заключалась в том, что он не учел эффект Томсона и соответствующую теплоту. Если учесть, что $T_1-T_2$- мала, ветви термопары короткие, то в первой ветви выделится теплота Томсона равная:
\[Q_{T1}={\sigma }_1I\left(T_1-T_2\right)\left(2.1\right).\]Во второй ветви поглотится количество теплоты равное:
\[Q_{T2}={\sigma }_2I\left(T_1-T_2\right)\left(2.2\right).\]Если это учесть, то равенство Клаузиуса можно записать как:
\[\frac{П_1}{T_1}-\frac{П_2}{T_2}+\left(\frac{{\sigma }_1}{T_1}-\frac{{\sigma }_2}{T_2}\right)\left(T_1-T_2\right)=0\left(2.3\right),\]где $П_1,\ П_2$ -- теплота Пельтье. Перейдем к дифференциальной форме, учтем, что $\left(T_1-T_2\right)$ -- мала, получим:
\[\frac{d}{dT}\frac{П}{T}=\frac{{\sigma }_2-{\sigma }_1}{T}\left(2.4\right)или\] \[\frac{П}{T}-\frac{dП}{dT}={\sigma }_1-{\sigma }_2\left(2.5\right).\]Тогда первое начало даст выражение:
\[П_1-П_2+\left({\sigma }_1-{\sigma }_2\right)\left(T_1-T_2\right)=\alpha \left(T_1-T_2\right)\left(2.6\right).\]Из (2.6) следует, что:
\[\frac{dП}{dT}+\left({\sigma }_1-{\sigma }_2\right)=\alpha \left(2.7\right).\]Из (2.5) и (2.7) получим, что:
\[П=\alpha T\to \alpha =\frac{П}{T}.\ \left(2.8\right),\]где коэффициент термоэлектродвижущей силы $\alpha $ -- не является постоянной величиной.
Ответ: $\alpha =\frac{П}{T}.$











