Эффект Доплера- изменение частоты и, соответственно, длины волны излучения, воспринимаемое наблюдателем, из-за движения источника излучения или движения наблюдателя.
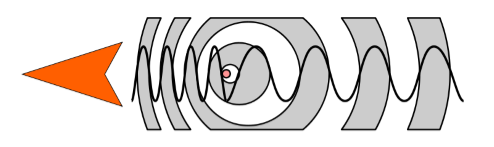
Рисунок 1. Изменение длины волны, вызванное движением источника
Для волн, распространяющихся в среде, таких как звуковые волны, эффект зависит от скорости наблюдателя и источника относительно среды, в которой эти волны распространяются. Таким образом, суммарный эффект Доплера может быть результатом движения источника, движения наблюдателя или движения среды. Каждый из этих эффектов анализируется отдельно.
В классической физике, где скорости источника и приемника относительно среды ниже, чем скорость волн в среде, связь между наблюдаемой частотой и источником частоты определяется по формуле:
где
${\rm c-\ }$ это скорость волн в среде;
${{\rm v}}_{{\rm r}}{\rm -}{\rm \ }$это относительная скорость приемника;
${{\rm v}}_{{\rm s}}{\rm -}$ относительная скорость источника.
Приведенная выше формула предполагает, что источник либо непосредственно приближается или удаляется от наблюдателя.
Если скорость, $v_s\ $а также $v_r\ $малы по сравнению со скоростью волны, отношения между наблюдаемой частотой и источником частоты можно записать:
Где
$\Delta v=v_r-v_s-$ это скорость приемника относительно источника: она положительна, когда источник и приемник движутся навстречу друг другу.

Рисунок 2. Эффект Доплера, наблюдаемый в потоке воды вокруг лебедя
Применение эффекта Доплера
-
Эффект Доплера для электромагнитных волн, таких как свет, имеет большое значение в астрономии и дает в результате так называемое красное смещение или синие смещение. Он был использован для измерения скорости, при которой звезды и галактики приближаются или удаляются от нас; то есть, их радиальные скорости.
Положительная радиальная скорость показывает, что звезда удаляется от Солнца, отрицательная, что она приближается.
-
Радар
Эффект Доплера используется в некоторых типах радаров для измерения скорости обнаруженных объектов. В радаре луч выстреливает по движущейся мишени - например, автомобилю, так как полиция использует радар для фиксирования скорости автомобилистов -- по мере приближения или удаления от радара.
-
Медицинская визуализация и измерение кровотока
Эхокардиограмма может, в определенных пределах, производить точную оценку направления кровотока и скорости крови и сердечной ткани в любой произвольной точке с использованием эффекта Доплера. Одним из недостатков является то, что ультразвуковой луч должен быть направлен параллельно потоку крови.
Измерения скорости кровотока также используются в других областях медицинского ультразвукового исследования, например в акушерском ультразвуковом исследовании, и неврологии. Измерение скорости кровотока в артериях и венах на основе эффекта Доплера является эффективным инструментом для диагностики сосудистых проблем, таких как стеноз.
При излучении спектра излучения некоторой туманности линия излучения водорода ${\lambda }_a=656,3\ нм$ оказалась смещенной на $\Delta \lambda =2,5\ нм$ в область с большей длиной волны (красное смещение). Определить скорость $v$ движения туманности относительно Земли и указать, удаляется она от Земли или приближается к ней.
Решение:
Эффект Доплера описывается формулой
\[U=U_0\frac{c}{c-v}\]Где
$v >0$ при приближении к наблюдателю
$v
Длина волны
\[\lambda =\frac{c}{v}\] \[\Delta \lambda =\lambda -{\lambda }_0=\frac{c}{U}-{\frac{c}{U}}_0=\frac{c-v}{U_0}-\frac{c}{U_0}=-\frac{v}{U_0}\ (1)\] \[U_0=\frac{c}{{\lambda }_0}=\frac{c}{{\lambda }_{\alpha }}\ (2)\]Подставим (2) в (1) и получим
\[\Delta \lambda =-\frac{v\cdot {\lambda }_{\alpha }}{c}\] \[v=-\frac{\Delta \lambda \cdot c}{{\lambda }_{\alpha }}\] \[v=-\frac{2,{10}^{-9}\cdot 3\cdot {10}^8}{656,3\cdot {10}^{-9}}=-1,14\cdot {10}^6{м}/{с}\]Ответ: туманность удаляется со скоростью $1,14\cdot {10}^6{м}/{с}$.











