По свои магнитным свойствам все вещества делятся на слабомагнитные и сильномагнитные. Кром того магнетики классифицируют в зависимости от механизма намагничивания.
Диамагнетики
Диамагнетики относят к слабомагнитным веществам. В отсутствии магнитного поля они не намагничены. В таких веществах при их внесении во внешнее магнитное поле в молекулах и атомах изменяется движение электронов так, что образуется ориентированный круговой ток. Ток характеризуют магнитным моментом ($p_m$):
где $S$ -- площадь витка с током.
Создаваемая этим круговым током, дополнительная к внешнему полю, магнитная индукция направлена против внешнего поля. Величина дополнительного поля может быть найдена как:
Диамагнетизмом обладает любое вещество.
Магнитная проницаемость диамагнетиков очень незначительно отличается от единицы. Для твердых тел и жидкостей диамагнитная восприимчивость имеет порядок приблизительно ${10}^{-5},\ $для газов она существенно меньше. Магнитная восприимчивость диамагнетиков не зависит от температуры, что было открыто экспериментально П. Кюри.
Диамагнетики делятся на «классические», «аномальные» и сверхпроводники. Классические диамагнетики имеют магнитную восприимчивость $\varkappa
В несильных магнитных полях намагниченность диамагнетиках пропорциональна напряженности магнитного поля ($\overrightarrow{H}$):
где $\varkappa $ -- магнитная восприимчивость среды (магнетика). На рис.1 представлена зависимость намагниченности «классического» диамагнетика от напряженности магнитного поля в слабых полях.
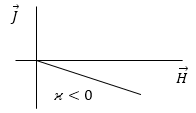
Рис.1
Парамагнетики
Парамагнетики, также относят к слабомагнитным веществам. Молекулы парамагнетиков имеют постоянный магнитный момент ($\overrightarrow{p_m}$). Энергия магнитного момента во внешнем магнитном поле вычисляется по формуле:
Минимальное значение энергии достигается тогда, когда направление $\overrightarrow{p_m}$ совпадает с $\overrightarrow{B}$. При внесении парамагнетика во внешнее магнитное поле в соответствии с распределением Больцмана появляется преимущественная ориентация магнитных моментов его молекул в направлении поля. Появляется намагничивание вещества. Индукция дополнительного поля совпадает с внешним полем и соответственно усиливает ее. Угол между направлением $\overrightarrow{p_m}$ и $\overrightarrow{B}$ не изменяется. Переориентирование магнитных моментов в соответствии с распределением Больцмана происходит за счет столкновений и взаимодействия атомов друг с другом. Парамагнитная восприимчивость ($\varkappa $) зависит от температуры по закону Кюри:
или закону Кюри -- Вейсса:
где C и C' -- постоянные Кюри, $\triangle $ - постоянная, которая бывает больше и меньше нуля.
Магнитная восприимчивость ($\varkappa $) парамагнетика больше нуля, но, как и у диамагнетика весьма мала.
Парамагнетики делят на нормальные парамагнетики, парамагнитные металлы, антиферромагнетики.
У парамагнитных металлов магнитная восприимчивость не зависит от температуры. Эти металлы слабомагнитны $\varkappa \approx {10}^{-6}.$
У парамагнетиков существует такое явление ка парамагнитный резонанс. Допустим, что в парамагнетике, который находится во внешнем магнитном поле, создают дополнительное периодическое магнитное поле, вектор индукции этого поля перпендикулярен вектору индукции постоянного поля. В результате взаимодействия магнитного момента атома с дополнительным полем создается момент сил ($\overrightarrow{M}$), который стремится изменить угол между $\overrightarrow{p_m}$ и $\overrightarrow{B}.$ Если частота переменного магнитного поля и частота прецессии движения атома совпадают, то созданный переменным магнитным полем момент сил либо все время увеличивает угол между $\overrightarrow{p_m}$ и $\overrightarrow{B}$, либо уменьшает. Это явление и называют парамагнитным резонансом.
В несильных магнитных полях намагниченность в парамагнетиках пропорциональна напряженности поля, и выражается формулой (3) (рис.2).
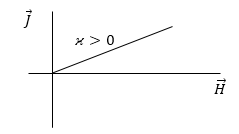
Рис. 2
Ферромагнетики
Ферромагнетики относят к сильномагнитным веществам. Магнетики, магнитная проницаемость которых достигает больших значений и зависит от внешнего магнитного поля и предшествующей истории называют ферромагнетиками. Ферромагнетики могут иметь остаточную намагниченность.
Магнитная восприимчивость ферромагнетиков является функцией от напряженности внешнего магнитного поля. Зависимость J(H) представлена на рис. 3. Намагниченность имеет предел насыщения ($J_{nas}$).
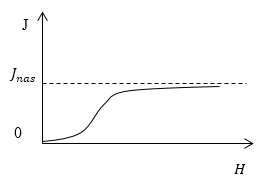
Рис. 3
Существование предела насыщения намагниченности указывает, что намагниченность ферромагнетиков вызвана переориентировкой некоторых элементарных магнитных моментов. У ферромагнетиков наблюдается явление гистерезиса (рис.4).
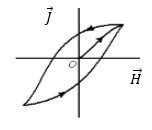
Рис. 4
Ферромагнетики в свою очередь делят на:
- Мягкие в магнитном отношении. Вещества с большой магнитной проницаемостью, легко намагничивающиеся и размагничивающиеся. Их используют в электротехнике, там, где работают с переменными полями, например в трансформаторах.
- Жесткие в магнитном отношении. Вещества с относительно небольшой магнитной проницаемостью, трудно намагничивающиеся и размагничивающиеся. Эти вещества используют при создании постоянных магнитов.
Задание: Зависимость намагниченности для ферромагнетика показана на рис. 3. J(H). Изобразите кривую зависимости B(H). Существует ли насыщение для магнитной индукции, почему?
Решение:
Так как вектор магнитной индукции связан с вектором намагниченности соотношением:
\[{\overrightarrow{B}=\overrightarrow{J\ }+\mu }_0\overrightarrow{H}\ \left(1.1\right),\]то кривая B(H) не достигает насыщения. График зависимости индукции магнитного поля от напряженности внешнего магнитного поля можно представить, как изображено на рис. 5. Такая кривая называется кривой намагничивания.
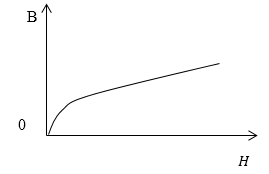
Рис. 5
Ответ: Насыщения для кривой индукции нет.
Задание: Получите формулу парамагнитной восприимчивости $(\varkappa)$, зная, что механизм намагничивания парамагнетика аналогичен механизму электризации полярных диэлектриков. Для среднего значения магнитного момента молекулы в проекции на ось Z можно записать формулу:
\[\left\langle p_{mz}\right\rangle =p_mL\left(\beta \right)\left(2.1\right),\]где $L\left(\beta \right)=cth\left(\beta \right)-\frac{1}{\beta }$ - функция Ланжевена при $\beta =\frac{p_mB}{kT}.$
Решение:
При высоких температурах и небольших полях, мы получим, что:
\[p_mB\ll kT,\ \to \beta \ll 1\ \left(2.2\right).\]Следовательно, при $\beta \ll 1$ $cth\left(\beta \right)=\frac{1}{\beta }+\frac{\beta }{3}-\frac{{\beta }^3}{45}+\dots $ , ограничение функции линейным членом по $\beta $ получим:
\[L\left(\beta \right)=\frac{\beta }{3}\left(2.3\right).\]Подставим в (2.1) результат (2.3), получим:
\[\left\langle p_{mz}\right\rangle =p_m\frac{p_mB}{3kT}=\frac{{p_m}^2B}{3kT}\ \left(2.4\right).\]Используя связь между напряженностью магнитного поля и магнитной индукцией ($\overrightarrow{B}=\mu {\mu }_0\overrightarrow{H}$), приняв во внимание, что магнитная проницаемость парамагнетиков мало отличается от единицы, можем записать:
\[\left\langle p_{mz}\right\rangle =\frac{{p_m}^2{\mu }_0H}{3kT}\left(2.5\right).\]Тогда намагниченность будет иметь вид:
\[J=n\left\langle p_{mz}\right\rangle =\frac{{p_m}^2{\mu }_0H}{3kT}n\ \left(2.6\right).\]Зная, что связь модуль намагниченности с модулем вектора напряженности имеет вид:
\[J=\varkappa H\ \left(2.7\right).\]Имеем для парамагнитной восприимчивости:
\[\varkappa =\frac{{p_m}^2м_0n}{3kT}\ .\]Ответ: $\varkappa =\frac{{p_m}^2{\mu }_0n}{3kT}\ .$











