Механизм намагничивания. Ларморова скорость
Диамагнетики относят к слабомагнитным веществам. В отсутствии магнитного поля они не намагничены. Рассмотрим в общих чертах механизм намагничивания. Это позволит установить причину разных знаков намагничения парамагнетиков и диамагнетиков, определить связь между атомным строением вещества и магнитной восприимчивостью.
Будем считать, что имеем дело с одноатомным газом. Если магнитное поле отсутствует, электроны в атоме движутся по круговой траектории вокруг ядра (r - ее радиус, ${\omega }_0-угловая\ скорость$). Центростремительная сила ($F_c$), которая действует на электрон, имеет вид:
Центростремительная сила имеет довольно большую величину в сравнении с силами, которые действуют на электрон со стороны внешних полей. Вследствие чего радиус окружности, по которой перемещается электрон, будем считать постоянным (В таком случае говорят, что атом жесткий).
Существует теорема Лармора согласно которой, изменение движения электрона в первом приближении сводится к наложению на движение без поля добавочного вращения (прецессии) всех электронов вокруг направления магнитного поля.
Итак, создаем вешнее магнитное поле, характер движения электронов изменяется. Внешнее поле направим перпендикулярно плоскости орбиты электрона. При этом сила Лоренца ($\overrightarrow{F}$) будет направлена вдоль радиуса орбиты и будет либо со направлена с $\overrightarrow{F_c}$, либо направлена против нее. По модулю, сила, с которой магнитное поле действует на частицу, равна:
\[F=q_e\omega rB\left(2\right),\]где $q_e$ -- заряд электрона по модулю, $\omega $ - угловая скорость движения электрона ($\omega \ne {\omega }_0$). Учитывая вышесказанное, уравнение движения электрона в поле имеет вид:
\[m{\omega }^2r=F_c\pm q_e\omega rB=m{{\omega }_0}^2r\pm q_e\omega rB\left(3\right),\]где знак ($\pm $) выбирают в зависимости от того как взаимно ориентированы векторы угловой скорости электрона и вектор магнитной индукции.
Используем то, что:
\[{\omega }^2-{\omega_0}^2=\left(\omega -\omega_0\right)\left(\omega +\omega_0\right)\approx 2\triangle \omega \omega ,\ \left|\triangle \omega \right|=\left|\omega -\omega_0\right|\ll \omega \ \left(4\right),\]тогда из (3) получим:
\[\triangle \omega =\pm \frac{q_eB}{2m}={\omega }_L\left(5\right).\]Мы получили, что в магнитном поле электрон получает дополнительную угловую скорость. Эту скорость называют ларморовой и обозначают ${\omega }_L$.
Если $\overrightarrow{B}$ направлен против угловой скорости движения электрона, то$\ \overrightarrow{F}\uparrow \downarrow \overrightarrow{F_c}$, следовательно, угловая скорость электрона уменьшится. Это значит, что ${\omega }_L\uparrow \uparrow \overrightarrow{B}$. Если направление $\overrightarrow{B}$ совпадает с угловой скоростью, то придем к такому же заключению, следовательно:
\[{\omega }_L=-\frac{q_eB}{2m}\left(6\right).\]В уравнении (6) учтено, что заряд электрона меньше нуля.
Ларморова прецессия
Для того чтобы понять каким будет движение атома при произвольной ориентации угловой скорости и индукции поля обобщим результат для произвольной ориентации угловой скорости и индукции поля. В таких веществах при их внесении во внешнее магнитное поле в молекулах и атомах изменяется движение электронов так, что образуется ориентированный круговой ток. Электрон, движущийся по орбите, аналогичен волчку. Ему свойственны все особенности поведения гироскопов при действии внешних сил. В частности, должна возникать прецессия электронной орбиты. Прецессия реализуется, если атом находится во внешнем магнитном поле $\overrightarrow{B}$. В поле на орбиту электрона действует вращательный момент равный:
\[\overrightarrow{N}=\left[\overrightarrow{p_m}\overrightarrow{B}\right]\left(7\right),\]где $\overrightarrow{p_m}$ -- орбитальный магнитный момент электрона. Вращательный момент стремится установить направление $\overrightarrow{p_m}$ по направлению поля (при этом механический момент $\overrightarrow{M}\ $ установится против поля). Под действием $\overrightarrow{N}$ векторы $\overrightarrow{p_m}$ и $\overrightarrow{M}\ $ совершают прецессию вокруг направления вектора $\overrightarrow{B}$.
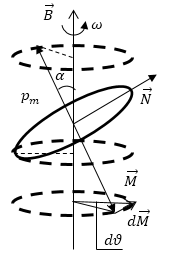
Рис. 1
За время dt вектор $\overrightarrow{M}$ получает приращение d$\overrightarrow{M}$, которое равно:
\[d\overrightarrow{M}=\overrightarrow{N}dt\left(8\right).\]Векторы $d\overrightarrow{M}$ и $\overrightarrow{N}$ перпендикулярны к плоскости, в которой лежат векторы $\overrightarrow{B}$ и $\overrightarrow{M}$. По модулю вектор $d\overrightarrow{M}$ равен:
\[dM=p_mBsin\alpha dt\ \left(9\right),\]где $\alpha $ -- угол между $\overrightarrow{p_m}$ и $\overrightarrow{B}$.
За время dt плоскость, в которой находится вектор $\overrightarrow{M}$ повернется вокруг направления вектора индукции на угол $d \vartheta$, равный:
\[d \vartheta=\frac{\left|d\overrightarrow{M}\right|}{Мsin\alpha }=\frac{p_mBsin\alpha dt}{Мsin\alpha }=\frac{p_mBdt}{М}\left(10\right).\]Величина $\frac{d \vartheta}{dt}={\omega }_L$ называется угловой скоростью прецессии. Из формулы (10) следует:
\[{\omega }_L=\frac{p_mB}{М}\left(11\right).\]Отношение $\frac{p_m}{М}$ называется магнитомеханическим (гиромагнитным) отношением, оно равно:
\[\frac{p_m}{М}=-\frac{q_e}{2m}\left(12\right),\]где m -- масса электрона, знак минус указывает, что направления моментов противоположны ($\overrightarrow{p_m}\uparrow \downarrow \overrightarrow{М}$). Подставим в (11) правую часть выражения (12), получим:
\[{\omega }_L=-\frac{q_eB}{2m}\left(13\right).\]Частоту ${\omega }_L$ называют частотой ларморовой прецессии (ларморовой частотой). Ларморова частота не зависит: от угла наклона орбиты относительно направления магнитного поля, от радиуса орбиты, скорости электрона. Она для всех электронов одинакова.
Прецессия вызывает дополнительное движение электрона вокруг направления поля. Дополнительное движение электронов порождает индуцированный магнитный момент атома (${p'}_{m\ at}$) равный:
\[{p'}_{m\ at}=-\frac{{q_e}^2B}{6m}\sum\limits^Z_{k=1}{\left\langle {r_k}^2\right\rangle \left(14\right),}\]где Z -- атомный номер химического элемента, число электронов в атоме равно Z. Индуцированный магнитный момент атома направлен против поля.
Ларморова прецессия возникает у всех веществ. К диамагнетикам относят такие вещества, у которых нет собственного магнитного момента.
Сущность диамагнетизма
В результате ларморовой прецессии каждый электрон в атоме можно уподобить круговому току. Этот ток составляет левовинтовую систему с направлением вектора индукции магнитного поля. Что означает, что дополнительная индукция, которая создается этим круговым, током направлена навстречу вектору индукции внешнего магнитного поля. Магнитный момент атома, который возникает в результате прецессии, и намагниченность направлены против вектора индукции внешнего магнитного поля. Возникновение ларморовой прецессии и связанных с ней магнитного момента и дополнительного поля -- сущность явления диамагнетизма.
Задание: Получите выражение для молярной магнитной восприимчивости диамагнетиков (${\varkappa }_{\mu }$). Оцените ее величину.
Решение:
Если величину ${p'}_{m\ at}$ умножить на число Авогадро ($N_A$), то получится магнитный момент моля вещества. Магнитная проницаемость диамагнетиков очень близка к единице. Следовательно, можно считать, что;
\[\overrightarrow{B}={\mu }_0\overrightarrow{H}\left(1.1\right).\]В таком случае молярную магнитную восприимчивость (${\varkappa }_{\mu }$) можно вычислить как:
\[{\varkappa }_{\mu }=\frac{N_A{p'}_{m\ at}}{H}=-\frac{{{{{\mu }_0N}_Aq}_e}^2}{6m}\sum\limits^Z_{k=1}{\left\langle {r_k}^2\right\rangle .}\]Вычисление величины:
\[\frac{{{{{\mu }_0N}_Aq}_e}^2}{6m}=3,55\cdot {10}^9.\]Радиусы электронных орбит имеют величину ${10}^{-10}м.$ Получается, что ${\varkappa }_{\mu }\sim {10}^{-10}\div {10}^{-11},\ $что согласуется с экспериментом.
Ответ: ${\varkappa }_{\mu }=-\frac{{{{{\mu }_0N}_Aq}_e}^2}{6m}\sum\limits^Z_{k=1}{\left\langle {r_k}^2\right\rangle .}{\varkappa }_{\mu }\sim {10}^{-10}\div {10}^{-11}.\ $
Задание: Если скорость электрона в атоме, который движется в магнитном поле, изменяется, следовательно, изменяется его кинетическая энергия. С другой стороны, если считать атом «жестким», потенциальная энергия неизменна. За счет чего изменяется скорость?
Решение:
Скорость электрона изменяться за счет работы постоянного магнитного поля не может, так как Лоренцова сила всегда перпендикулярна вектору магнитной индукции внешнего поля. Следовательно, стационарное магнитное поле работы над электроном не производит. Однако, при появлении магнитного поля возникает электрическое поле, под действием которого и изменяется скорость движения электрона в атоме.












