Кинематика изучает механическое движение частиц без учета причин, вызывающих изменение характера движения частиц (сил). Закон движения частиц системы считается заданным. По этому закону в кинематике определяются скорости, ускорения, траектории движения частиц системы.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Если все части тела движутся одинаково, то есть любая прямая, связанная с движущимся телом, остаётся при движении параллельной сама себе, то такое движение называется поступательным движением.
Движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называется вращательным движением.
В общем случае тело при движении описывает некую кривую. Такое движение называется криволинейным движением. Любое криволинейное движение можно представить как комбинацию поступательных и вращательных движений.
Закон движения,задающий положение материальной точки в пространстве в любой момент времени, можно определять либо координатным способом, через зависимость координат от времени x = x (t), y = y (t), z = z (t), либо векторным способом, через зависимость от времени радиус-вектора $\overrightarrow{r}=\overrightarrow{r}\left(t\right)$, проведенного из начала координат к данной точке (рис. 1.1).
Поскольку радиус-вектор можно представить как линейную комбинацию базисных векторов системы отсчёта$\ \overrightarrow{i},\ \overrightarrow{\ j},\ \overrightarrow{k}$, в которой коэффициентами служат координаты точки, справедливо соотношение: $\overrightarrow{r}\left(t\right)=$ x (t) $\overrightarrow{i}$+ y (t) $\overrightarrow{j}+z (t)\ \overrightarrow{k}$. Это равенство называется кинематическим уравнением движения точки в векторной форме.
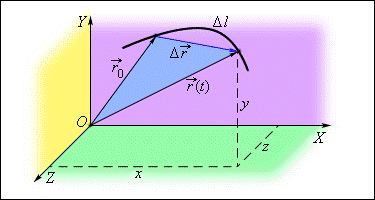
Рисунок 1.1
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус-вектора $\overrightarrow{r}\left(t\right)$.
$\overrightarrow{r_0\ }$-- радиус-вектор положения точки в начальный момент времени.
Перемещением тела $\overrightarrow{s}=\triangle \overrightarrow{r}=\overrightarrow{r}-\overrightarrow{r_0\ }$ называют направленный отрезок прямой, соединяющий начальную и конечную точки траетктории тела. Перемещение - величина векторная. Пройденный путь l равен длине траектории, пройденной телом за некоторое время t. Путь -- скалярная величина.

Рисунок 1.2.
Пройденный путь l и вектор перемещения $\overrightarrow{s}$ при кривoлинейном движении тела. $a$ и $b$ - начальная и конечная точки пути.
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.2).












