Скорость

Источник статьи

Автор24 — учеба по твоим правилам

Определение

Скоростью в механике называется физическая величина, характеризующая зависимость перемещения тела от времени, в течение которого осуществлялось это перемещение. В наиболее упрощённой форме эта зависимость отражена в понятии средней скорости:

$\overrightarrow{v}=\frac{\triangle \overrightarrow{s}}{\triangle t}=\frac{\triangle \overrightarrow{r}}{\triangle t}$

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени $\Delta$ t: $\overrightarrow{v}={\mathop{lim}_{\triangle t\to 0} \frac{\triangle \overrightarrow{s}}{\triangle t}\ }=\frac{d\overrightarrow{r}}{dt}=\dot{\overrightarrow{r}}$

Декартовых координатах это уравнение эквивалентно системе трёх уравнений:

$\left\{ \begin{array}{c} v_x=\frac{dx}{dt}=\dot{x} \\ v_y=\frac{dy}{dt}=\dot{y} \\ v_z=\frac{dz}{dt}=\dot{z} \end{array} \right.$

где $v_x$ , $v_y$ , $\ v_z$ -- проекции вектора $\overrightarrow{v}$ на координатные оси. Модуль вектора $\overrightarrow{v}$ :

$v=\left|\overrightarrow{v}\right|=\sqrt{v^2_x+v^2_y+v^2_z}=\sqrt{x^2+y^2+z^2}$

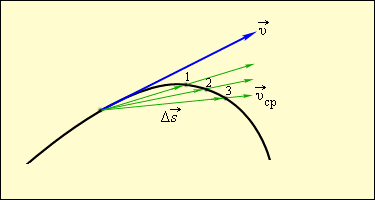
Средняя и мгновенная скорости

Рисунок 1. Средняя и мгновенная скорости

Мгновенная скорость $\overrightarrow{v}$ тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.

При движении тела по криволинейной траектории его скорость $\overrightarrow{v}$ изменяется по модулю и направлению. Изменение вектора скорости $\overrightarrow{v}$ за некоторый малый промежуток времени $\Delta$ t можно задать с помощью вектора $\triangle \overrightarrow{v}$ (рис. 2.)

Вектор изменения скорости $\triangle \overrightarrow{v}=\ \overrightarrow{v_2}-\ \overrightarrow{v_1}$ за малое время $\Delta$ t можно разложить на две составляющие:

$\triangle \overrightarrow{v_{\tau }}$ , направленную вдоль вектора $\overrightarrow{v}$ (касательная составляющая), и $\triangle \overrightarrow{v_n}\$ , направленную перпендикулярно вектору $\overrightarrow{v}$ (нормальная составляющая).

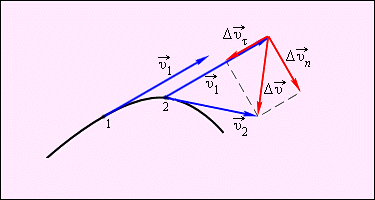
Изменение вектора скорости по величине и направлению

Рисунок 2.

Изменение вектора скорости по величине и направлению: $\triangle \overrightarrow{v}=\ \overrightarrow{v_{\tau }}+\ \overrightarrow{v_n}$ -- изменение вектора скорости за время $\triangle t$

Единицей измерения скорости в системе СИ является метр в секунду: $\left[v\right]=м/c$

Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра $q_1,q_2,\ q_3$ , называемых криволинейными, или обобщенными координатами, которые также однозначно определяют положение точки в пространстве.

Скорость точки М при задании ее движения в криволинейных координатах определится в виде векторной суммы составляющих скоростей, параллельных координатным осям: $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{\partial \overrightarrow{r}}{\partial q_1}\dot{q_1}+\frac{\partial \overrightarrow{r}}{\partial q_2}\dot{q_2}+\frac{\partial \overrightarrow{r}}{\partial q_3}\dot{q_3}=v_{q_1}\overline{e_1}+v_{q_2}\overline{e_2}\ +v_{q_3}\overline{e_3}$

Проекции вектора скорости на соответствующие координатные оси равны:

$v_{q_i}=\overline{v\ }\cdot \overline{e_i}=H_i\dot{q_i}\ \ ,\ \ i=\overline{1,3}$

Здесь $H_i=\left|{\left(\frac{\partial \overrightarrow{r}}{\partial q_i}\right)}_M\right|$ - параметр, который называется i-ым коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов $\overline{e_i}$ имеет направление, соответствующее направлению движения точки конца радиус-вектора $r_i$ при возрастании i-ой обобщенной координаты. Модуль скорости в ортогональной криволинейной системе координат можно рассчитать по зависимости:

$v=\sqrt{v^2_{q_1}+v^2_{q_2}+v^2_{q_3}}=\sqrt{H^2_1{\dot{q_1}}^2+H^2_2{\dot{q_2}}^2+H^2_3{\dot{q_3}}^2}$

В приведенных формулах значения производных и коэффициентов Ламе вычисляют для текущего положения точки М в пространстве.

Координатами точки в сферической системе координат являются скалярные параметры r, ${\mathbf \varphi },\ {\mathbf \theta }$ , отсчитываемые так, как показано на рис. 3

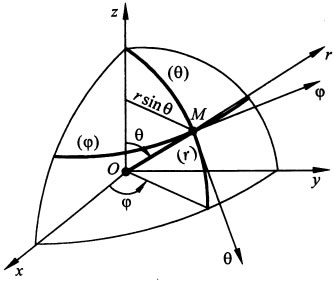
Изменение вектора скорости по величине и направлению

Рисунок 3. Вектор скорости в сферической системе координат

Система уравнений движения точки в данном случае имеет вид:

$\left\{ \begin{array}{c} r=r(t) \\ \varphi =\varphi (t \\ \theta =\theta (t \end{array} \right.$

На рис.3 изображены радиус-вектор $r$ , проведенный из начала координат, углы ${\mathbf \varphi }$ и ${\mathbf \theta }$ , а также координатные линии и оси рассматриваемой системы в произвольной точке М траектории. Видно, что координатные линии $({\mathbf \varphi })$ и $({\mathbf \theta })$ лежат на поверхности сферы радиусом r. Данная криволинейная система координат также является ортогональной. Декартовы координаты могут быть выражены через сферические координаты так:

$x=rcos\varphi sin\theta ;\ \ y=rsin\varphi cos\theta ;\ \ z=rcos\theta \ \$

Тогда коэффициенты Ламе: $H_r=1;\ \ H_{\varphi }=rsin\varphi ;\ \ H_0=r$ ;

проекции скорости точки на оси сферической системы координат $v_r=\dot{r\ \ };\ \ v_{\varphi }=rsin\varphi ;\ \ v_{\theta }=r\theta \ \$ , а модуль вектора скорости $v=\sqrt{v^2_r+v^2_{\varphi }+v^2_{\theta }}=\sqrt{{\dot{r}}^2+r^2{\dot{\varphi }}^2+r^2{\dot{\theta }}^2}$