Что такое изохорический процесс
Изохорическим (или изохорным) процессом называется процесс, происходящий в неизменной массе газа при постоянном объеме. Запишем уравнение для двух состояний идеального газа:
Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:
или
Уравнение (4) называют законом Шарля.
Этот процесс происходит с подводом тепла, если давление увеличивается, или его отводом, чтобы уменьшать давление. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:
Из определения работы газа очевидно, что в изохорном процессе она равна 0:
$dA=0,\ $A=0 (6).
Соответственно:
где $\delta Q\ $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, i-число степеней свободы молекулы газа, R -- универсальная газовая постоянная, d - количество молей газа.
Изменение внутренней энергии газа:
где $c_{\mu V}$ -- молярная теплоёмкость газа при изохорном процессе. Уравнение (9) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $\triangle T.$
Изображение изопроцессов
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изохорический процесс, называется изохорой (рис.1).
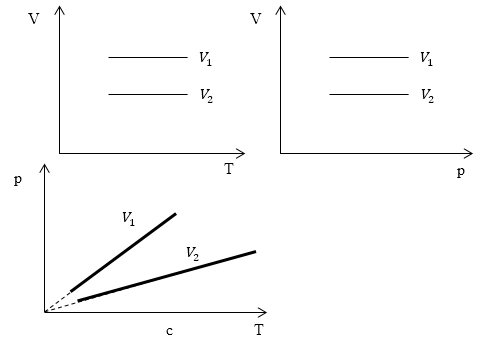
Рис. 1
Задание: Определите, как соотносятся объемы $V_1$ и $V_2$ на диаграмме p(T) рис 1с.
Решение:
Проведем изотерму $T_1$, которая пересечет изохоры в точках A и B.
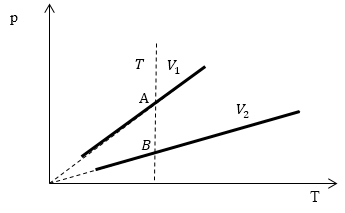
Рис. 2
В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля -- Мариотта:
\[p_AV_A=p_BV_B\ (1.2)\] \[p_A > p_B \to V_A Ответ: Объем $V_1 > V_2$.Задание: Сравнить изменение объема газа в процессах I и II (рис.3). Масса газа не изменяется.
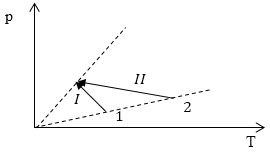
Рис. 3
Решение:
Рассмотрим рисунок (рис.3). Линии, обозначенные пунктиром -- изохоры. Все точки, лежащие на изохоре, определяют состояния газа с одинаковыми объемами. Это значит, что объемы газа (начальные для процессов I и II) одинаковы ($V_{I1}=V_{II1}$). Аналогичная ситуация со второй пунктирной линией -- это изохора. Следовательно, $V_{I2}=V_{II2}$. Так как начальные и конечные объемы процессов I и II равны, то и их изменение одинаково:
\[{\triangle V}_I=\triangle V_{II}.\]Ответ: Изменения объемов в процессах I и II одинаковы.
Задание: На рис. 4 представлен процесс при постоянном объеме и переменной массе идеального газа. Как изменяется масса газа в этом процессе?
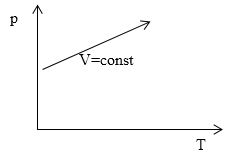
Рис. 4
Решение:
В этой задаче следует прежде всего обратить внимание, что мы имеем дело не с изопроцессом, не смотря на то, что объем постоянен, так как масса идеального газа переменна.
Уравнение процесса, исходя из графика, можно записать в виде:
\[p=a+bT\ \left(3.1\right).\]Запишем уравнение Менделеева -- Клайеперона для идеального газа:
\[pV=\frac{m}{\mu }RT\ \left(3.2\right),\]где m масса газа, $\mu $- молярная масса газа.
Выразим из (3.2) массу:
\[m=\frac{pV\mu }{RT}\ \left(3.3\right).\]Подставим (3.1) в (3.2), получим:
\[m=\frac{(a+bT\ )V\mu }{RT}=\frac{aV\mu }{RT}+\frac{bV\mu }{R}\left(3.3\right).\]В случае $V=const$ второе слагаемое в уравнении (3.3) с увеличением температуры постоянно. Первое слагаемое при увеличении T уменьшается. Следовательно, в процессе на рис. 4 (при увеличении температуры и соответственно, давления) масса газа уменьшается.
Ответ: В заданном процессе масса газа уменьшается.











