Фазовая скорость
Монохроматическая волна вида:
является бесконечной во времени и пространстве последовательностью «горбов и впадин», которые распространяются по оси $X$. Причем фазовая скорость перемещения максимумов и минимумов равна:
Скорость $v$ -- означает скорость перемещения фазы. Используя такую волну нельзя передать сигнал, так как все «горбы» эквивалентны. Для того чтобы передавать сигнал следует сделать на волне «метку» (например сделать некоторый обрыв на конечное время $\triangle t$). Но при этом волна уже не будет соответствовать уравнению (1).
Сигнал можно передать, используя импульс света. По теореме Фурье его можно разложить в ряд с частотами в интервале $\triangle \omega .$ Совокупность волн, которые различаются друг с другом, частотой в пределах малого интервала $\triangle \omega $ называют волновым пакетом (группой волн). Аналитически волновой пакет можно представить как:
где индекс $\omega $ у величин $A,\ k,\ \alpha $ показывает, что они относятся к разным частотам. В пределах пакета плоские волны усиливают друг друга, вне пакета происходит взаимное гашение волн. Для того чтобы сумму волн, которую описывает выражение (3), можно было считать пакетом, должно выполняться условие: $\triangle \omega \ll {\omega }_0.$
Групповая скорость
При отсутствии дисперсии все плоские волны в пакете распространяются с фазовой скоростью $v$. При таких условиях скорость распространения группы волн совпадает с фазовой скоростью, форма пакета постоянна. В веществе при наличии дисперсии пакет со временем ширина пакета увеличивается. При малой дисперсии, скорость перемещения центра пакета (точка, в которой максимальна величина $E$) называют групповой скоростью $(u).$ Групповая скорость характеризует импульс, и соответствует скорости распространения энергии поля этого импульса или скорость перемещения амплитуды.
При наличии дисперсии групповая и фазовая скорость различны:
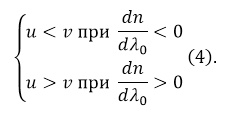
Рисунок 1.
Если пакет представлен двумя составляющими, то групповую скорость можно найти как:
Групповая скорость пакета волн, который задан уравнением (3) может быть определена как:
если в разложении функции $k_{\omega }=k_0+{\left(\frac{dk}{d\omega }\right)}_0\left(\omega -{\omega }_0\right)+\dots \left(7\right)$ пренебречь членами высоких порядков. В выражении ${\left(\frac{dk}{d\omega }\right)}_0$- производная в точке ${\omega }_0$. В формуле (6) индекс $0$ опущен, так как не требуется. В таком приближении форма пакета волны постоянна во времени. Если в разложении (7) учесть следующие члены, то пакет волны будет расплываться.
Выражение для групповой скорости (6) можно записать в виде:
Связь групповой и фазовой скоростей (формула Рэлея)
Выражение для групповой скорости можно записать в виде:
Формула (9) называется формулой Рэлея. В том случае, если $\frac{dv}{d\lambda } >0$ имеют дело с нормальной дисперсией, и $uv$. Выражение (9) можно представить как:
Выражение (10) показывает зависимость групповой скорости от характеристик вещества.
При введении понятия групповой скорости используют случай, когда дисперсия не велика. В противном случае пакет волн быстро деформируется и само понятие групповой скорости не имеет смысла. К примеру, около полосы поглощения среды, в области существенного изменения фазовой скорости в зависимости от частоты формула (9) может дать величину $u$ больше, чем скорость света в вакууме, или отрицательное значение. То есть в такой области формула Рэлея не применима.
Задание: Представьте групповую скорость в виде функции от показателя преломления и длины волны. Чему равна групповая скорость волн в воде, если ${\lambda }_1$=656,3 нм. Считайте, что при $t=20{\rm^\circ\!C}$ показатель преломления для этой длины воны $n_1=1,3311$, для ${\lambda }_2=643,8$ нм $n_{12}=1,3314.$
Решение:
За основу решения задачи примем определение групповой скорости:
\[u=\frac{d\omega }{dk}\left(1.1\right).\]Зная, что круговая частота связана с длинной волны соотношением:
\[\omega =\frac{2\pi с}{n\lambda }\left(1.2\right).\]Волновой вектор можно записать как:
\[k=\frac{2\pi }{\lambda }\left(1.3\right).\]Подставим выражения (1.2) и (1.3) в (1.1), получим:
\[u=\frac{d\left(\frac{2\pi с}{n\lambda }\right)}{d\left(\frac{2\pi }{\lambda }\right)}=c\frac{(nd\lambda +\lambda dn)/n^2{\lambda }^2}{d\lambda /{\lambda }^2}=\frac{c}{n}\left(1+\frac{\lambda }{n}\frac{dn}{d\lambda }\right)\left(1.4\right).\]Подставим данные из условий задачи, проведем вычисления:
\[u=\frac{3\cdot {10}^8}{1,3311}\left(1+\frac{656,3}{1,3311}\frac{0,0003}{12,5}\right)=2,28\cdot {10}^8\left(\frac{м}{с}\right).\]Ответ: $u\left(n,\lambda \right)=\frac{c}{n}\left(1+\frac{\lambda }{n}\frac{dn}{d\lambda }\right)=2,28\cdot {10}^8\frac{м}{с}.$
Задание: Найдите выражение групповой скорости ($u$), если фазовая скорость ($v$) представлена выражением: $v=a{\lambda }^q,$ где $a=const,\ q
Решение:
В качестве основы для решения задачи используем формулу Рэлея, определяющую групповую скорость вида:
Используя уравнение изменения фазовой скорости, заданное в условиях задачи найдем $\frac{dv}{d\lambda }$, имеем:
Подставим (2.2) в формулу Рэлея, получим:
Ответ: $u=v(1-q)$.












