Что такое потенциальное поле
Поле (для любых сил) называется потенциальным (консервативным), если работа при перемещении в нем зависит только от конечной и начальной точки пути и не зависит от траектории движения тела. Существует и другое, но абсолютно равнозначное определение потенциальности поля. Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равна нулю.
Нам известно, что сила гравитации ($F_G\sim \frac{1}{r^2}$), которая убывает обратно пропорционально квадрату расстояния, является потенциальной, причем ее потенциальность обусловлена именно такой зависимостью от расстояния. Сила Кулона также, обратно пропорциональна квадрату расстояния, мы помним закон Кулона ($F_E\sim \frac{1}{r^2}$), тоже потенциальна. Все математическое описание потенциала было создано при исследовании сил гравитации. Понятие о потенциале возникло в работах Ж.Л. Лагранжа в 1777 г. Термин «потенциал» ввели в науку гораздо позднее Дж. Грин и К.Ф. Гаусс.
На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля. Математически доказать это очень просто. Циркуляция вектора напряженности поля точечного заряда ($\overrightarrow{E_i}$) по любому замкнутому контуру равна нулю:
\[\oint\limits_L{\overrightarrow{E_i}d\overrightarrow{s}=0\ \left(1\right).}\]Если поле создается N точечными зарядами, то по принципу суперпозиции мы можем результирующее поле найти как:
\[\overrightarrow{E}=\sum\nolimits_i{\overrightarrow{E_i}}\ \left(2\right).\]Найдем интеграл:
\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=\oint\limits_L{\sum\nolimits_i{\overrightarrow{E_i}}}d\overrightarrow{s}=\sum\nolimits_i{\oint\limits_L{\overrightarrow{E_i}d\overrightarrow{s}}}=\sum\nolimits_i{0}=0\ \left(3\right).}\]Выше описанный критерий потенциальности поля не является дифференциальным, вследствие чего, его бывает трудно применять. Приходится проверять равенство нулю работы по замкнутому контуру. Это значит необходимо исследовать бесконечное количество циклов, что, в конечном счете, невозможно. Критерий потенциальности можно применить только тогда, когда известна аналитическая формула работы, что бывает совсем не всегда. Следовательно, необходимо найти другой критерий потенциальности поля, который был бы легок в применении. Таким критерием стала дифференциальная формулировка. Она дается с помощью понятия ротор вектора ($rot\overrightarrow{A}$).
Что такое ротор
Ротором называют вектор, проекция которого на направление единичного вектора $\overrightarrow{n}$ определяется следующим образом:
\[{rot}_n\overrightarrow{A}={\mathop{lim}_{\triangle S\to 0} \frac{\oint{\overrightarrow{A}\cdot d\overrightarrow{s}}}{\triangle S}\ }\left(4\right),\]где $\triangle S$- площадь, лежащая в плоскости перпендикулярной к $\overrightarrow{n}$, которая ограничена малым контуром $L$, на контуре $L$ --направление положительного обхода связано с $\overrightarrow{n}$ правилом правого винта.
(Обратите внимание, что здесь большой буквой $S$ обозначается площадь, маленько буквой $s$ -- линейное перемещение.)
Ротор характеризует интенсивность «завихрения» вектора. При практическом вычислении ротора используют формулы:
\[rot\ \overrightarrow{A}=\overrightarrow{\nabla }\times \overrightarrow{A}=\left| \begin{array}{ccc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ A_x & A_y & A_k \end{array} \ \right|\left(5\right).\]Независимость работы от пути перемещения заряда в электростатическом поле выражается равенством:
\[\int\limits^B_{ \begin{array}{c} A \\ L_1 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}}=\int\limits^B_{ \begin{array}{c} A \\ L_2 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}\ \left(6\right),}\]где $L_1\ и\ L_2$ различные пути между точками А и В. Учтем, что при замене местами пределов интегрирования получим:
\[\int\limits^B_{ \begin{array}{c} A \\ L_2 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}=-\int\limits^A_{ \begin{array}{c} B \\ L_2 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}\ ,}\left(7\right),}\]Выражение (6) представим как:
\[\int\limits^B_{ \begin{array}{c} A \\ L_1 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}+\int\limits^A_{ \begin{array}{c} B \\ L_2 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}=\oint\limits_L{\overrightarrow{E}\cdot d\overrightarrow{s}}=0\ (8),}}\]где $L=L_1+L_2$. Применим формулу Стокса:
\[\int\limits_S{rot}\overrightarrow{A}\cdot d\overrightarrow{S}=\oint\limits_L{\overrightarrow{A}\cdot d\overrightarrow{s}(9)}\]к уравнению (8), получим:
\[\oint\limits_L{\overrightarrow{E}\cdot d\overrightarrow{s}}=\int\limits_S{rot\overrightarrow{E}\cdot d\overrightarrow{S}}=0\ \left(9\right),\]где $S$ -- поверхность, которая ограничена контуром $L$. Так как поверхность произвольна, то интеграл в выражении (9) может быть равен нулю, только если равно нулю подынтегральное выражение, а так как $d\overrightarrow{S}\ne 0$ то есть:
\[rot\overrightarrow{E}=0\left(10\right).\]Формула (10) является дифференциальной формулировкой потенциальности электростатического поля.
Задание: Найти $rot_n\overrightarrow{v}\ $для точек оси вращения, если $\overrightarrow{v}$ -- вектор скорости точек твердого тела, которое вращается с угловой скоростью $\omega$ вокруг оси коллинеарной $\overrightarrow{n}$.
Решение:
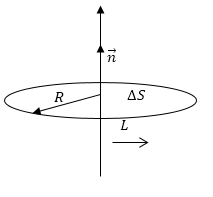
Рис. 1
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рис.1). Мы знаем, что:
\[v=\omega R\left(1.1\right),\] \[\triangle S=\pi R^2\left(1.2\right).\]Определим, что такое $vds$. $ds$- скалярное значение элемента окружности. Поэтому, используем формулу -- определение ротора, получаем:
\[{rot}_n\overrightarrow{v}={\mathop{lim}_{R\to 0} \frac{\oint{\overrightarrow{\omega R}\cdot d\overrightarrow{s}}}{\pi R^2}\ }={\mathop{lim}_{R\to 0} \frac{\omega R2\pi R}{\pi R^2}\ }=2\omega \ \left(1.3\right),\]где $\oint{ds}=2\pi R$- длина окружности.
Ответ: Ротор линейной скорости точек вращающегося тела равен ${rot}_n\overrightarrow{v}=2\omega .$
Задание: Доказать, что из условия потенциальности поля следует, что тангенциальные составляющие напряженности электростатического поля не прерываются.
Решение:
Так как электростатическое поле потенциально, то выполняется равенство:
\[A=\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=0\ \left(2.1\right).}\]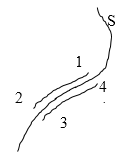
Рис. 2
Тангенциальные составляющие -- это касательные к произвольной поверхности в любой ее точке. Непрерывность означает, что касательные составляющие напряженности имеют одинаковые значения по обе стороны поверхности. Допустим обратное. Пусть вдоль поверхности S (рис.2) непрерывность не выполняется. Это значит, что если 1,2 и 3,4 разделенные поверхностью S, но при этом бесконечно близкие друг к другу точки, то работа электростатических сил на пути $1\to 2$ отличается на конечную величину от работы тех же сил на пути $3\to 4$. Так как мы считаем, что отрезки $1\to 2$ и $3\to 4$ бесконечно малые, силы конечны, следовательно, и работа, выполняемая электрическими силами на заданных отрезках -- бесконечно малая величина. Получается, что работа на пути $1\to 2\to 3\to 4\to 1$ должна быть не равна нулю. То есть работа сил по перемещению пробного заряда по замкнутому контуру не равна нулю. Такое невозможно, так как электростатическое поле потенциальное. Мы показали, что тангенциальные составляющие напряженности электростатического поля ненепрерывны.











