Что такое граничные условия
Граничными условиями называют связь между векторами, характеризующими поле, по разные стороны поверхности, которая разграничивает две области. Такая поверхность может разделять вещества, обладающие различными свойствами, может отделять вещество от вакуума, может быть воображаемой границей.
В любом случае граничные условия позволяют определить изменения векторов поля при переходе через границу. Их получают с помощью уравнений поля.
Уравнения поля
Если два разных диэлектрика находятся в электрическом поле, то на их границе возникают поверхностные заряды. Это понятно, при одинаковой напряженности электрического поля поляризованность разных диэлектриков различна. Значит, граница диэлектриков пересекается разным количеством поляризационных зарядов со стороны каждого диэлектрика. В конечном итоге около границы собирается некоторый связанный заряд, который является поверхностным зарядом, его поверхностную плотность будем обозначать ${\sigma }_{sv}$. Так, при переходе через границу двух различных диэлектриков можно записать следующее выражение:
\[-\left(P_{2n}-P_{1n}\right)={\sigma }_{sv}\left(1\right),\]где $P_{2n}$-нормальная составляющая вектора поляризации диэлектрика с номером 2, $P_{1n}$ - нормальная составляющая вектора поляризации диэлектрика с номером 1. Граничное условие для вектора поляризации (1) можно записать несколько иначе:
\[-\overrightarrow{n_2}\left(\overrightarrow{P_2}-\overrightarrow{P_1}\right)={\sigma }_{sv}\left(2\right),\]$\overrightarrow{n_2}$-единичный вектор нормали, который направлен из первой во вторую среду. $\overrightarrow{P_2},\overrightarrow{P_1}$. Формулы (1,2) могут применяться и для границы диэлектрик -- вакуум (для вакуума поляризованность полагается равной нулю), то есть $P_{2n}=0$, получим в таком случае:
\[P_n={\sigma }_{sv}\ \left(3\right),\]где $P_n$ -- перпендикулярная составляющая вектора поляризации на границе диэлектрика с вакуумом.
При переходе через границу раздела двух диэлектриков для нормальной составляющей вектора $\overrightarrow{D}$ можно записать:
\[D_{2n}-D_{1n}=\sigma \ \left(4\right).\]или
\[\overrightarrow{n_2}\left(\overrightarrow{D_2}-\overrightarrow{D_1}\right)=\sigma \ \left(5\right),\]где $\sigma $ -- поверхностная плотность распределения свободных зарядов на границе диэлектриков. $\overrightarrow{n_2}$ -- нормаль, которая проведена в сторону второй среды. Если свободных зарядов на границе раздела двух диэлектриков нет, то:
\[D_{2n}=D_{1n}\left(6\right).\]Для тангенциальной составляющей:
\[D_{2\tau }=\frac{{\varepsilon }_2}{{\varepsilon }_1}D_{1\tau }\left(7\right),\]где ${\varepsilon }_2$, ${\varepsilon }_1$ -- диэлектрические проницаемости диэлектриков.
Нормальная же составляющая напряженности электрического поля на границе двух диэлектриков терпит разрыв (силовые линии преломляются). Если около границы нет свободных зарядов, то можно записать:
\[{\varepsilon }_1E_{1n}={\varepsilon }_2E_{2n}\left(8\right).\]В том случае если ${\varepsilon }_2>{\varepsilon }_1$, следовательно, $E_{2n}
Граничные условия для тангенциальной составляющей вектора напряженности ($E_{\tau }$) при переходе из одного диэлектрика в другой имеют вид:
\[E_{2\tau }-E_{1\tau }=0\ \to E_{2\tau }=E_{1\tau }\left(9\right).\]Граничные условия выполняются для полей изменяющихся во времени. Эти условия справедливы и для границы с вакуумом. Надо только помнить, что диэлектрическая проницаемость вакуума полагается равна единице.
Задание: Объясните, как ведет себя поле (с точки зрения рисунка силовых линий), если в него внести шаровой слой диэлектрика с достаточно большой диэлектрической проницаемостью (рис.1).
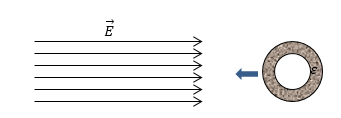
Рис. 1
Решение:
При переходе через границу раздела воздух -- диэлектрик силовые линии поля преломляются. Так как воздух имеет меньшую диэлектрическую проницаемость, чем шаровой слой, то силовые линии удаляются от нормали к границе шарового слоя. Если полый диэлектрик с большой диэлектрической проницаемостью внести в электрическое поле, то вследствие преломления линии поля будут концентрироваться преимущественно в слое диэлектрика. Внутри полости они расположатся редко. Поле внутри полости будет ослаблено в сравнении с внешним полем. Полость обладает экранирующим действием. Однако экранирование не является полным. Чем больше $\varepsilon $, тем больше экранирующее действие (рис.2).
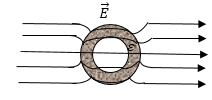
Рис. 2
Задание: Получите закон преломления линий электрического смещения при переходе границы между двумя диэлектриками (рис.3).
Решение:
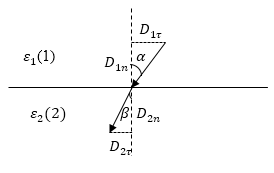
Рис. 3
Основой для решения задачи станет тот факт, что линии смещения электрического поля ($\overrightarrow{D}$) проходят границу раздела двух диэлектриков не прерываясь (рис.3). Количество линий приходящих к площадке $\triangle S$ из диэлектрика с номером (1) будет равно:
\[D_1\triangle S_1=D_1\triangle Scos\alpha \ \left(2.1\right).\]Количество линий выходящих из площадки $\triangle S$ в диэлектрик с номером (2) равно:
\[D_2\triangle S_2=D_2\triangle Scos\beta \ \left(2.2\right).\]Так как линии не претерпевают разрыва, то из количества должны быть одинаковы, то есть запишем, что:
\[D_1\triangle Scos\alpha =D_2 \triangle Scosв\ \ \left(2.3\right),\]где
\[D_1cos\alpha =D_{1n},\ D_2cos\beta =D_{2n}\left(2.4\right).\]На границе диэлектриков линии электрического смещения терпят преломление, угол между нормалью к поверхности раздела и линией электрического смещения изменяется ($\alpha \to \beta $). Из рис 3. следует, что
\[\frac{tg\alpha }{tg\beta }=\frac{D_{1\tau }}{D_{1n}}:\frac{D_{2\tau }}{D_{2n}}\left(2.5\right).\]А мы знаем, что:
\[\frac{D_{2\tau }}{D_{1\tau }}=\frac{{\varepsilon }_2}{{\varepsilon }_1},\ D_{1n}=D_{2n}\left(2.6\right),\ \]следовательно, подставляя граничные условия для составляющих вектора смещения в (2.5) получим закон преломления линий электрического смещения:
\[\frac{tg\alpha }{tg\beta }=\frac{D_{1\tau }}{D_{2\tau }}\cdot \frac{D_{1n}}{D_{2n}}=\frac{{\varepsilon }_1}{{\varepsilon }_2}.\]Ответ: Мы получили искомый закон преломления:$\frac{tg\alpha }{tg\beta }=\frac{{\varepsilon }_1}{{\varepsilon }_2}.$











