Что такое диэлектрики
Диэлектриками называют вещества, которые не способны проводить электрический ток.
Изоляторов, которые абсолютно не проводят электрический ток, в природе не существует. Диэлектрики в $10^{15} -10^{20}$ раз хуже проводят ток, чем проводники. Дело в том, что в диэлектриках отсутствуют свободные заряды.
Если диэлектрик внести в электрическое поле, то и поле, и сам диэлектрик сильно изменяются. В изначально не заряженных диэлектриках в присутствии поля возникают электрические заряды. Происходит явление поляризации вещества, то есть на диэлектрике в поле возникают электрические полюсы. Заряды, которые появляются при этом, называют поляризационными зарядами. Отделить друг от друга поляризационные заряды не возможно. В этом состоит их существенное отличие от индукционных зарядов в проводниках. Такое отличие объясняется тем, что в металлах присутствуют электроны, которые могут перемещаться на значительные расстояния. В диэлектриках положительные и отрицательные заряды связаны между собой и могут смещаться только в пределах одной молекулы, то есть на очень небольшие расстояния.
Диэлектрики состоят или из нейтральных молекул, или из заряженных ионов, которые закреплены в положениях равновесия, например в узлах кристаллической решетки. Ионные кристаллические решетки могут быть разбиты на «элементарные ячейки», которые в целом нейтральны.
Под действие электрического поля, в отличие от проводников, заряды в диэлектрике не срываются полем со своего места, а только слегка смещаются. Диэлектрик в отсутствии электрического поля условно можно представить как совокупность молекул, в каждой из которых положительные и отрицательные заряды равные по величине распределены по всему объему вещества. В состоянии поляризации диэлектрика заряды каждой молекулы смещаются в противоположные стороны, таким образом, один конец молекулы становится положительно заряженным, другой отрицательно. То есть молекула превращается в электрический диполь. Равнодействующая электрических сил, которые действуют на нейтральную молекулу диэлектрика в однородном поле, равна нулю, так как центр тяжести молекулы остается неподвижным. Молекула просто деформируется.
Существуют диэлектрики, в которых молекулы имеют дипольный момент в отсутствии электрического поля (полярные молекулы). Если поле отсутствует, то полярные молекулы участвуют в тепловом движении, ориентированы беспорядочно. При внесении диэлектрика в поле, молекулы ориентируются в основном в направлении поля. Следовательно, диэлектрик поляризуется. У симметричных молекул, например, $O_2,\ N_2,$ при отсутствии поля центы тяжести отрицательных и положительных зарядов совпадают, вследствие, чего собственного дипольного момента у молекул нет (неполярные молекулы). У несимметричных молекул (${например,\ H}_2O,\ CO$) центры тяжести сдвинуты друг относительно друга, в результате чего молекулы имеют дипольный момент и называются полярными.
Существуют диэлектрические кристаллы (ионные кристаллы), которые строятся из ионов противоположного знака. Подобный кристалл состоит из двух кристаллических решеток, положительной и отрицательной, вдвинутых одна в другую. Кристалл в целом можно уподобить гигантской молекуле. При наложении электрического поля происходит сдвиг одной решетки относительно другой, так происходит поляризация ионных кристаллов. Существуют кристаллы, которые поляризованы и без поля. При дальнейшем изучении поведения диэлектриков в электрических полях механизм возникновения поляризации значения иметь не будет. Существенным является лишь то, что поляризация диэлектрика проявляется через возникновение некомпенсированных макроскопических зарядов. Когда диэлектрик не поляризован, объемная плотность его зарядов ($\rho $) и поверхностная плотность ($\sigma $) равны нулю. В результате поляризации $\sigma \ne 0$, а иногда и $\rho \ne 0.$ Поляризация сопровождается возникновением в тонком поверхностном слое диэлектрика избытка связанных зарядов одного знака. В том случае, если перпендикулярная составляющая напряженности поля $\overrightarrow{E_n}\ne 0$ на выделенном участке, то под действием поля заряды одного знака уходят внутрь, а другого выходят наружу.
Вектор поляризации
Степень поляризации диэлектрика характеризуется поляризованностью ($\overrightarrow{P}$) или вектором поляризации:
\[\overrightarrow{P}=\frac{\overrightarrow{\triangle p}}{\triangle V}\ \left(1\right),\]где $\overrightarrow{\triangle p}$ -- дипольный момент элемента диэлектрика. Для неполярных молекул вектор поляризованности можно определить, как:
\[\overrightarrow{P}=\frac{1}{\triangle V}\sum\limits_{\triangle V}{\overrightarrow{p_i}}=N\overrightarrow{p_0}\ \left(2\right),\]где суммирование идет относительно всех молекул в объеме $\triangle V$. $N$ -- концентрация молекул, $\overrightarrow{p_0}$ -- индуцированный дипольный момент (Он одинаковый у всех молекул). $\overrightarrow{p_0}\uparrow \uparrow \overrightarrow{E}.$
Формула поляризованности для полярных молекул имеет вид:
\[\overrightarrow{P}=\frac{1}{\triangle V}\sum\limits_{\triangle V}{\overrightarrow{p_i}}=N\left\langle \overrightarrow{p}\right\rangle \left(3\right),\]где $\left\langle \overrightarrow{p}\right\rangle $ -- среднее значение дипольных моментов, которые равны по модулю, но разнонаправлены. В изотропных диэлектриках средние дипольные моменты совпадают по направлению с напряженностью внешнего электрического поля. У диэлектриков с полярного типа молекулами, вклад в поляризованность от наведенных зарядов много меньше, чем вклад от переориентации поля.
Ионная решеточная поляризации описывается формулой (3). В большинстве случаев такая поляризация является анизотропной.
Если представить плоский конденсатор, который заполнен диэлектриком (рис.1), то на левой обкладке его находится положительный заряд, на правой -- отрицательный. Так как притягиваются разноименные заряды, то у положительной обкладки возникнет на поверхности диэлектрика отрицательный заряд, а у правой (отрицательной) -- положительный заряд диэлектрика. Получается, что поле, которое создают поляризационные заряды, направлено против поля, которое создают обкладки, то есть диэлектрик ослабляет поле.
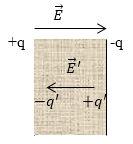
Рис. 1
$+q, -q$ -- заряды на обкладках конденсатора.
$\overrightarrow{E}$ -- напряженность поля, которое создается обкладками конденсатора.
$-q',\ +q'$ -заряды диэлектрика.
$\overrightarrow{E}'$ - напряженность поля, которое создается в результате поляризации диэлектрика.
Влияние вещества на электрические и магнитные поля было открыто Фарадеем эмпирически. Именно он ввел в науку термины диэлектрик и диэлектрическая постоянная.
Если однородный изотропный диэлектрик заполняет полностью объем, который ограничен эквипотенциальными поверхностями поля сторонних зарядов, то напряженность поля внутри диэлектрика в $\varepsilon $ раз меньше, чем напряженность поля сторонних зарядов.
\[\overrightarrow{E'}=\overrightarrow{\frac{E}{\varepsilon }}\ \left(4\right),\]где $\varepsilon $ -- диэлектрическая проницаемость среды.
Напряженность поля точечного заряда, который находится в диэлектрике с диэлектрической проницаемостью $\varepsilon$, равна:
\[\overrightarrow{E}=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{q}{r^3}\overrightarrow{r}\left(5\right).\]Закон Кулона для зарядов, находящихся в жидком и газообразном диэлектрике имеет вид:
\[\overrightarrow{F}=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{\left|q_1\right|\left|q_2\right|}{r^3}\overrightarrow{r}\ \left(6\right).\]Задание: Бесконечную плоскую пластину из однородного изотропного диэлектрика поместили в однородное электростатическое поле напряженностью $E=200\frac{В}{м}$ перпендикулярно силовым линиям поля. Диэлектрическая проницаемость диэлектрика равна 2. Какова напряженность поля внутри диэлектрика.
Решение:
Поле в вакууме в $\varepsilon $ раз сильнее, чем в диэлектрике, поэтому запишем, что:
\[\overrightarrow{E'}=\overrightarrow{\frac{E}{\varepsilon }}\ \]Проведем расчет:
\[E'=\frac{200}{2}=100\left(\frac{В}{м}\right).\]Ответ: Напряженность поля в пластине будет 100$\frac{В}{м}$.
Задание: Заряженные шарики имеют массы $m_1=m_2=m.\ Они\ $подвешены на нитях одинаковой длины в одной точке, их заряды равны $q_1$ и $q_2$.(рис.1). Сначала они находятся в воздухе (диэлектрическая проницаемость ${\varepsilon }_1$) за тем погружены в жидкость ${\varepsilon }_{2.}$ Каково отношение диэлектрических проницаемостей $(\frac{{\varepsilon }_{2.}}{{\varepsilon }_1})$, если при погружении в жидкость системы из шариков угол расхождения нитей не изменился? Отношение плотности шариков к плотности диэлектрика ($\frac{{\rho }_{sh}}{{\rho }_d}$)=b.
Решение:
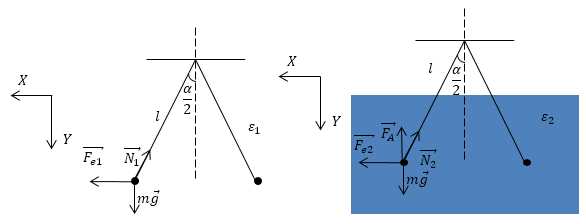
Рис. 2 и 3
Запишем условие равновесия шарика (одного, так как система симметрична) в воздухе:
\[\overrightarrow{F_{e1}}+\overrightarrow{mg}+\overrightarrow{N_1}=0\ \left(2.1\right).\]Запишем условие равновесия шарика (одного) в жидкости:
\[\overrightarrow{F_{e2}}+\overrightarrow{mg}+\overrightarrow{N_2}+\overrightarrow{F_A}=0\ \left(2.2\right).\]Запишем проекции уравнения (2.1.) на оси:
Ох: $F_{e1}-N_1sin(\frac{\alpha }{2})$=0 (2.3),
Oy: $mg-N_1cos(\frac{\alpha }{2})$=0 (2.4).
Проекции уравнения (2.2) на оси:
Ох: $F_{e2}-N_2sin(\frac{\alpha }{2})$=0 (2.5),
Oy: $mg-N_2cos {\left(\frac{\alpha }{2}\right)\ }-F_A=0\ \left(2.6\right).$
Разделим уравнение (2.3) на (2.4), получим:
\[tg\left(\frac{\alpha }{2}\right)=\frac{F_{e1}}{mg}\ \left(2.7\right).\]Уравнение (2.5) на уравнение (2.6), имеем:
\[tg\left(\frac{\alpha }{2}\right)=\frac{F_{e2}}{mg-F_A}\to \frac{F_{e1}}{mg}=\frac{F_{e2}}{mg-F_A}\left(2.8\right).\]По закону Кулона запишем выражения для $F_{e1},\ F_{e2}$:
\[F_{e1}=\frac{q_1q_2}{4\pi {\varepsilon }_1{\varepsilon }_0r^{2\ \ }}и\ F_{e2}=\frac{q_1q_2}{4\pi {\varepsilon }_2{\varepsilon }_0r^{2\ \ }}\ \left(2.9\right).\]Модуль силы Архимеда равен:
\[F_A={\rho }_dVg={\rho }_d\frac{m}{{\rho }_{sh}}g\ \left(2.10\right).\]Подставим в уравнение (2.8) уравнения (2.9) и (2.10), получим:
\[\frac{\frac{q_1q_2}{4\pi {\varepsilon }_1{\varepsilon }_0r^{2\ \ }}}{mg}=\frac{\frac{q_1q_2}{4\pi {\varepsilon }_2{\varepsilon }_0r^{2\ \ }}}{mg-{\rho }_d\frac{m}{{\rho }_{sh}}g\ }\to \frac{\frac{1}{{\varepsilon }_1}}{1}=\frac{\frac{1}{{\varepsilon }_2}}{1-\frac{{\rho }_d}{{\rho }_{sh}}\ }\to \frac{{\varepsilon }_2}{{\varepsilon }_1}=\frac{1}{1-\frac{{\rho }_d}{{\rho }_{sh}}}=\frac{1}{1-b}.\]Ответ: Диэлектрическая проницаемость жидкости должна быть $\frac{{\varepsilon }_2}{е_1}=\frac{1}{1-b}$.











