Сила тяжести. Вес. Закон Галилея

Закон Галилея

Галилей впервые выяснил, что тяжелые предметы падают вниз так же быстро, как и легкие. Чтобы проверить это предположение Галилео Галилей сбрасывал с Пизанской башни в один и тот же момент пушечное ядро массой $80$ кг и значительно более легкую мушкетную пулю массой $200$ г. Оба тела имели примерно одинаковую обтекаемую форму и достигли земли одновременно. До него господствовала точка зрения Аристотеля, который утверждал, что легкие тела падают с высоты медленнее тяжелых.

Рисунок 1.

Такова легенда. В архивах не сохранилось никаких подтверждений, что такой эксперимент действительно проводился. Более того, пушечное ядро и пуля имеют разный радиус, на них будет действовать разная сила сопротивления воздуха и, поэтому, они не могут достичь земли одновременно. Это понимал и Галилей. Однако он писал, что

"...различие в скорости движения в воздухе шаров из золота, свинца, меди, порфира и других тяжелых материалов настолько незначительно, что шар из золота при свободном падении на расстоянии в одну сотню локтей наверняка опередил бы шар из меди не более чем на четыре пальца. Сделав это наблюдение, я пришел к заключению, что в среде, полностью лишенной всякого сопротивления, все тела падали бы с одинаковой скоростью".

Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая:

• Все тела при падении движутся одинаково: начав падать одновременно, они движутся с одинаковой скоростью;
• Движение происходит с постоянным ускорением.

Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью.

Сила тяжести и вес

Под действием силы притяжения к Земле все тела падают с одинаковым относительно поверхности Земли ускорением, которое принято обозначать буквой $g$.

Это означает, что в системе отсчета, связанной с Землей, на всякое тело массы $m$ действует сила $P=mg$ называемая силой тяжести.

Когда тело покоится относительно поверхности Земли, сила $P$ уравновешивается реакцией $F$, подвеса или опоры, удерживающих тело от падения $F=-P$.

По третьему закону Ньютона тело в этом случае действует на подвес или опору с силой $G$, равной $-F$, т. е. с силой:

Сила $G$, с которой тело действует на подвес или опору, называется весом тела. Эта сила равна $mg$ лишь в том случае, если тело и опора (или подвес) неподвижны относительно Земли. В случае их движения с некоторым ускорением $a$ вес $G$ не будет равен $mg$.

Это можно уяснить на следующем примере. Пусть подвес в виде укрепленной на рамке пружины движется вместе с телом с ускорением $a$.

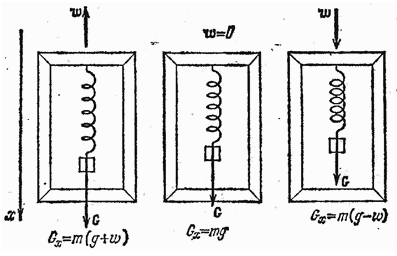
Рисунок 2.

Тогда уравнение движения тела будет иметь вид:

где $F$ - реакция подвеса, т. е. сила, с которой пружина действует на тело. По третьему закону Ньютона тело действует на пружину с силой, равной $-F$ которая по определению представляет собой вес тела $G$ в этих условиях. Заменив реакцию $F$, силой $-G$, а силу тяжести $P$ - произведением $mg$ получим:

$G=m(g-a)$. (1)

Формула 91) определяет вес тела в общем случае. Она справедлива для подвеса или опоры любого вида.

Предположим, что тело и подвес движутся в вертикальном направлении.

Спроектируем (1) на направление отвеса:

$G=m(g\pm a)$. (2)

В этом выражении $G$, $a$, $g$ суть модули соответствующих векторов. Знак $\pm$ соответствует $a$, направленному вверх либо вниз.

Из формулы (2) вытекает, что по модулю вес $G$ может быть как больше, так и меньше, чем сила тяжести $P$. При свободном падении рамки с подвесом $a=g$ и сила $G$, с которой тело действует на подвес, равна нулю. Наступает состояние невесомости. Космический корабль, летящий вокруг Земли с выключенными двигателями, движется, как и свободно падающая рамка, с ускорением $g$, вследствие чего тела внутри корабля находятся в состоянии невесомости - они не оказывают давления на соприкасающиеся с ними тела.

В случае неподвижной опоры силы $P$ и $G$ совпадают по величине и по направлению (обе они равны $mg$). Однако следует помнить, что эти силы приложены к разным телам: $P$ приложена к самому телу, $G$ приложена к подвесу или опоре, ограничивающим свободное движение тела в поле сил земного тяготения. Кроме того, сила $P$ всегда равна $mg$независимо от того, движется тело или покоится, сила же веса $G$ зависит от ускорения, с которым движутся опора и тело, причем она может быть как больше, так и меньше $mg$.

Ускорение свободного падения $g$ и сила тяжести $P$ зависят от широты местности. Кроме того, они зависят также от высоты над уровнем моря - с удалением от центра Земли они уменьшаются.