Описание сути явления
Возникновение разности потенциалов в проводнике с током под воздействием магнитного поля называют эффектом Холла.
Электропроводность металлов зависит от концентрации электронов проводимости (n) и их подвижности (b). Данные величины являются весьма важными характеристиками металла и определяются опытным путем. Так, для измерения концентрации электроном используют эффект Холла. Рассмотрим проводник в виде прямоугольной пластины, в которой течет ток плотности $\overrightarrow{j.}$ Эквипотенциальными поверхностями внутри этой пластины являются плоскости, перпендикулярные направлению тока, следовательно, разность потенциалов на рис.1 между точками (1 и 2) равна нулю.
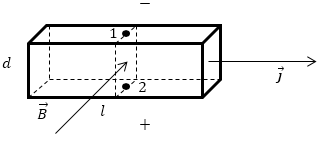
Рис. 1
Если в металле создать магнитное поле, которое будет перпендикулярно току, то между точками 1 и 2 (рис.1) возникнет разность потенциалов, которая говорит о том, что при наличии магнитного поля эквипотенциальные поверхности в пластинке отклоняются от первоначального положения. В возникновении поперечной разности потенциалов заключается эффект Холла.
Сущность эффекта Холла
Эффект Холла является следствием существования силы Лоренца. На движущиеся в магнитном поле заряды действует сила Лоренца. Под ее действием электрон отклоняется от первоначального направления движения к одной из граней. В результате одна из граней проводника заряжается отрицательно, следовательно, другая становится положительно заряженной. Внутри металла появляется поперечное электрическое поле ($\overrightarrow{E_x}$).
Сущность этого явления заключена в том, что электропроводимость проводника во внешнем магнитном поле является тензорной величиной (не скаляром). Напряженность поперечного электрического поля, которое называют холловским, добавляется к напряженности электрического поля, которое вызывает ток в отсутствии магнитного поля. В результате $\overrightarrow{E}$ поля образует с плотностью тока угол, который называют углом Холла (направление вектора $\overrightarrow{E}$ и направление вектора $\overrightarrow{j\ }\ $ не совпадают). Связь напряжённости и плотности тока имеет вид:
где ${\sigma }_{ik}$ -- тензор электропроводимости. Эффект Холла относят к гальваномагнитным эффектам (эффектам, которые происходят в веществе под действие магнитного поля).
Эмпирически получено, что поперечная разность потенциалов (U), возникающая в эффекте Холла в слабых магнитных полях, может быть рассчитана как:
где $R=\frac{1}{nq_e}$- постоянная Холла, $q_e$ -- заряд электрона. Разность потенциалов измеряется, остальные величины в формуле (1) известны. Так находится концентрация зарядов. По знаку разности потенциалов определяют знак носителей тока.
Значение и применение эффекта Холла
Результаты измерений показали, что в металлах ток происходит как движение отрицательных зарядов (электронов). Концентрация их изменяется в пределах равенства концентрации атомов. То есть на один атом вещества приходится, в среднем, один свободный электрон. У металлов концентрация атомов около $n\sim {10}^{28}м^{-3}.$
Эффект Холла наблюдается не только в металлах, но и например, в полупроводниках. Опыты по изучению эффекта Холла в разных веществах показали, что он не всегда является результатом движения отрицательных зарядов. Если измерение разности потенциалов в эффекте Холла показывает, что движутся положительные заряды, то такой эффект называют аномальным.
Эффект Холла используют создавая так называемые датчики Холла. Они используются для определения параметров магнитных полей, нахождения местоположения объектов.
Данный эффект используют для изучения энергетического спектра носителей заряда в металлах и полупроводниках.
На эффекте Холла основано действие магнитных насосов для стимулирования циркуляции жидких металлов и других проводящих жидкостей и магнитодинамических генераторов энергии.
Для измерения постоянной Холла часто применяют компенсационный метод. Составляют цепь, которая изображена на рис.2. По пластинке А течет ток, к ней подведены два контакта 1 и 2. G -- гальванометр, K -- компенсатор, который создает напряжение противоположное напряжению Холла. Изменяют напряжение с помощью компенсатора добиваются того, чтобы ток через гальванометр обратился в ноль. Получают, что разность потенциалов на компенсаторе и напряжение холла совпали. Используя формулу (2) рассчитывают постоянную $R$. В справочных материалах иногда приводят две постоянных Холла расчетную и экспериментальную. Расхождения объясняются тем, что в расчетах предполагается, что число электронов проводимости в точности равно количеству валентных электронов. $R$ может быть как положительной так и отрицательной. Постоянная Холла считается положительной, если векторы $\overrightarrow{j},\ \overrightarrow{B},\ {\overrightarrow{E}}_x$ образуют правовинтовую систему.
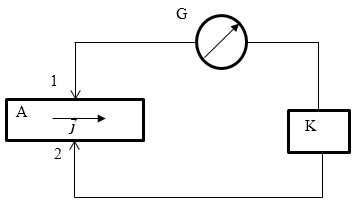
Рис. 2
Задание: Рассчитайте холловскую разность потенциалов для золотой ленты толщины $l={10}^{-4}$ м, по которой течет ток 10 А. Магнитное поле $1Тл.$
Решение:
Для решения задачи используем формулу:
\[U=RdjB\ \left(1.1\right),\]где экспериментальное значение постоянной Холла $R_{Au}$=-0,7$\cdot {10}^{-11}\frac{м^3}{Кл}$. Плотность тока ($j$) найдем как:
\[j=\frac{I}{ld}\left(1.2\right).\]Подставим (1.2) в (1.1), получим:
\[U=R\frac{I}{l}B.\]Проведем вычисления:
\[U=-7,4\cdot {10}^{-11}\frac{10}{{10}^{-4}}\cdot 1=-7,4\cdot {10}^{-6}\left(В\right).\]Ответ: Холловская разность потенциалов весьма мала, и составляет $U=7,4\cdot {10}^{-6}В.$
Задание: Получите выражение для постоянной Холла, считая, что проводник с током, помещен в магнитное поле. Следует допустить, что электрон движется равномерно.
Решение:
Сила Лоренца, которая действует на электрон в магнитном поле, движущийся со скорость $\overrightarrow{v}$ равна:
\[\overrightarrow{F}=q_e\overrightarrow{E}+q_e\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.1\right).\]В равновесии $\overrightarrow{F}=0$ тогда можно записать, что:
\[q_e\overrightarrow{E}={-q}_e\left[\overrightarrow{v}\overrightarrow{B}\right]\to \overrightarrow{E}=-\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.2\right).\]Плотность тока в проводнике можно выразить как:
\[\overrightarrow{j}=-q_en\overrightarrow{v}\left(2.3\right),\]где $n$ -- концентрация электронов. Из $\left(2.3\right)$ выразим скорость:
\[\overrightarrow{v}=-\frac{\overrightarrow{j}}{nq_e}\left(2.4\right).\]Кроме того разность потенциалов между точками 1- 2 (рис.1) равна:
\[d\cdot \overrightarrow{E}=U\left(2.5\right).\]Подставим в (2.5) выражение для напряженности (2.2) и скорость из (2.4), получим:
\[U=d\left[\frac{\overrightarrow{j}}{nq_e}\overrightarrow{B}\right]=\frac{d}{nq_e}\left[\overrightarrow{j}\overrightarrow{B}\right]\left(2.6\right).\]Выражение для разности потенциалов в эффекте Холла имеет выражение:
\[U=RdjB\left(2.7\right).\]Получаем, что постоянная Холла равна:
\[R=\frac{1}{nq_e}.\]Ответ: $R=\frac{1}{nq_e}.$


















