Марковские случайные процессы — это случайные процессы, эволюция которых при любом заданном значении временного параметра, не зависит от эволюции, предшествующей им, при наличии условия, что значение процесса в данный момент является зафиксированным.
Введение
Считается очень удобным отображать появление случайных событий в форме вероятностей переходов из одного состояния системы в другое, поскольку при этом предполагается, что, после перехода в текущее состояние, система может не учитывать в дальнейшем причины и обстоятельства того, как она попала в данное состояние.
Случайный процесс именуется Марковским процессом, то есть, процессом без последействия, когда для любого момента времени t вероятность какого-либо состояния системы в будущем может зависеть лишь от ее текущего состояния и не имеет зависимости от того, как система попала в это состояние. То есть, Марковский процесс считается удобным представлять в виде графа переходов из состояния в состояние. Известны следующие варианты описания Марковских процессов:
- Описание с дискретным временем.
- Описание с непрерывным временем.
В первом варианте переход из одного состояния в другое осуществляется в заранее известные моменты времени, то есть, такты (1, 2, 3, 4, …). Переход реализуется в каждом такте, то есть, специалиста при этом может интересовать только очередность состояний, которую преодолевает случайный процесс в своем развитии, и не интересует, в какие конкретно моменты осуществляется каждый из переходов. Во втором варианте специалист интересуется и цепочкой сменяющих друг друга состояний, и моментами времени, в которые осуществлялись данные переходы. Следует также отметить, что когда вероятность перехода не имеет временной зависимости, то Марковская цепь считается однородной.
Марковские случайные процессы
Модель Марковского процесса с дискретным временем может быть представлена как граф, в котором состояния, то есть вершины, связаны между собой связями, являющимися переходами из i-го состояния в j-е состояние, как показано в примере на рисунке ниже.

Рисунок 1. Граф. Автор24 — интернет-биржа студенческих работ
Любой переход может быть охарактеризован вероятностью перехода Pij. Вероятность Pij может показать, как часто после прихода в i-е состояние выполняется далее переход в j-е состояние. Естественно, подобные переходы могут происходить случайно, но если взять частоту переходов за достаточно большой период времени, то скорее всего данная частота совпадет с найденной вероятностью перехода. Очевидно, что у любого состояния суммарное значение вероятностей всех переходов, то есть, исходящих стрелок из него в другие состояния, обязано всегда быть равным единице, как показано в примере на рисунке ниже.

Рисунок 2. Граф. Автор24 — интернет-биржа студенческих работ
А полностью граф может быть представлен как показано в следующем примере.
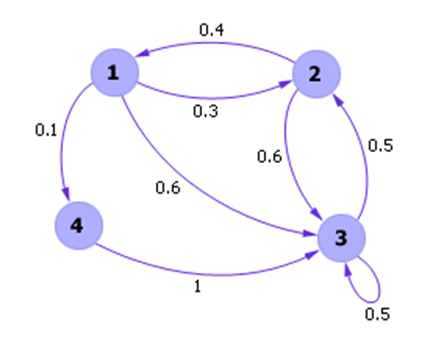
Рисунок 3. Граф. Автор24 — интернет-биржа студенческих работ
Осуществление Марковского процесса, то есть, процесс его моделирования, является вычислением последовательности (цепочки) переходов из состояния в состояние. Цепь на рисунке выше выступает как случайная последовательность и может иметь также и иные варианты реализации.
Для того чтобы определить, в какое следующее состояние может перейти процесс из текущего i-го состояния, следует выполнить разбиение интервала [0; 1] на подынтервалы размером $P_{i1}, P_{i2}, P_{i3}, … (P_{i1} + P_{i2} + P_{i3} + … = 1)$, как показана на следующем рисунке.

Рисунок 4. Подынтервыалы. Автор24 — интернет-биржа студенческих работ
Затем при помощи генератора случайных чисел (ГСЧ) необходимо определить следующее равномерно распределенное в интервале $[0; 1]$ случайное число $r_{рр}$ и найти, в какой из интервалов оно попадет. Далее реализуется переход в состояние, определенное ГСЧ, и повторение указанной процедуры для очередного состояния. Итогом работы модели должна стать Марковская цепь, как на рисунке ниже.

Рисунок 5. Марковская цепь. Автор24 — интернет-биржа студенческих работ
Рассмотрим пример имитация стрельбы из пушки по цели. Для имитации стрельбы из пушки по цели, выполним построение модели Марковского случайного процесса. Введем определение следующих трех состояний:
- Состояние $S_0$, которое означает, что цель не повреждена.
- Состояние $S_1$, которое означает, что цель повреждена.
- Состояние $S_2$, которое означает, что цель разрушена.
Далее следует задать вектор начальных вероятностей:

Рисунок 6. Вектор начальных вероятностей. Автор24 — интернет-биржа студенческих работ
Значение P0 для всех состояний призвано показать, какова вероятность каждого из состояний объекта перед началом стрельбы. Затем следует задать матрицу перехода состояний, как показано ниже.

Рисунок 7. Матрица перехода состояний. Автор24 — интернет-биржа студенческих работ
Матрица может задавать вероятность перехода из любого состояния в любое другое. Следует отметить, что вероятности задаются таким образом, что суммарное значение вероятностей перехода из одного состояния во все другие всегда должно равняться единице, ведь куда-нибудь система перейдет в любом случае. Наглядная модель Марковского процесса может быть представлена в виде графа, изображенного ниже.

Рисунок 8. Граф. Автор24 — интернет-биржа студенческих работ
При помощи данной модели и метода статистического моделирования, можно найти решение следующей задачи, а именно, найти среднее число снарядов, которое будет необходимо для того, чтобы полностью разрушить цель.
Выполним имитацию процесса стрельбы при помощи таблицы случайных чисел. Предположим, что начальным состоянием было $S_0$. Зададим следующую последовательность из таблицы случайных чисел:
0.32, 0.54, 0.22, 0.41, 0.62, 0.23, …
Данные случайные числа призваны обозначить следующие состояния:
- 0.32 обозначает, что цель находится в состоянии $S_0$ и остается в состоянии $S_0$, поскольку 0 ∠ 0.32 ∠ 0.45;
- 0.54 обозначает, что цель находится в состоянии $S_0$ и переходит в состояние $S_1$, поскольку 0.44 ∠ 0.53 ∠ 0.44 + 0.41;
- 0.22 обозначает, что цель находится в состоянии $S_1$ и остается в состоянии $S_1$, поскольку 0 ∠ 0.22 ∠ 0.44;
- 0.41 обозначает, что цель находится в состоянии $S_1$ и остается в состоянии $S_1$, поскольку 0 ∠ 0.41 ∠ 0.44;
- 0.62 обозначает, что цель находится в состоянии $S_1$ и переходит в состояние $S_2$, поскольку 0.44 ∠ 0.62 ∠ 0.44 + 0.56.
Поскольку достигнуто состояние $S_2$ (дальше цель будет переходить из $S_2$ в состояние $S_2$ с вероятностью, равной единице), то цель считается пораженной. Для этого в приведенном примере потребовалось пять снарядов.












