Перед выполнением арифметических действий операнды операции помещаются в соответствующие регистры арифметико-логического устройства.
Сложение и вычитание
Перед выполнением сложения и вычитания необходимо выполнение выравнивания порядков:
Мантисса числа с меньшим порядком сдвигается в своем регистре вправо на такое количество разрядов, которое равно разности порядков операндов. После каждого сдвига порядок увеличивается на $1$.
После выравнивания порядков чисел одноименные разряды располагаются в соответствующих разрядах обоих регистров, что позволяет выполнить дальнейшее сложение или вычитание мантисс. Если в результате выполнения операций получен не нормализованный результат, то его необходимо нормализовать сдвигом мантиссы результата влево и одновременным уменьшением порядка результата.
Алгоритм выполнения сложения (вычитания) вещественных чисел $A$ и $B$:
-
Выровнять порядки:
а) найти разность порядков $\triangle P=P_A-P_B$;
б) если $\triangle P >0$, то сдвинуть мантиссу числа $B$ на $\triangle P$ разрядов вправо; если $\triangle P
-
Выполнить сложение (вычитание) мантисс и произвести округление по $n+1$-му разряду.
-
Присвоить результату порядок большего числа.
-
Нормализовать (если есть необходимость) мантиссу суммы (разности) с одновременным изменением порядка.
Сложить нормализованные числа ${0,11011}_2\cdot 2^8$ и ${0,10001}_2\cdot 2^{10}$.
-
Выровняем порядки:
а) разность порядков $\triangle P=8-10=-2$;
б) $\triangle P

Рисунок 1.
В результате получили нормализованное число с порядком большего числа.
Выполнить вычитание нормализованных чисел ${0,10001}_2\cdot 2^{10}$ и ${0,11011}_2\cdot 2^8$.
-
Выровняем порядки:
а) разность порядков $\triangle P=10-8=2$;
б) $\triangle P >0$, поэтому мантиссу второго числа сдвинем вправо на $2$ разряда:
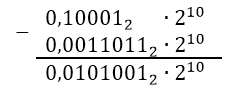
Рисунок 2.
В результате получили не нормализованное число, поэтому его мантиссу сдвигаем влево на $1$ разряд и уменьшаем порядок на $1$: ${0,101001}_2\cdot 2^9$.
Найти сумму чисел $32,875$ и $4,5$ в двоичной системе счисления.
Переведем данные числа в двоичный код:
\[{32,875}_{10}={0010\ 0000,111}_2={0,100000111}_2\cdot 2^{110};\] \[{4,5}_{10}={0000\ 0100,1}_2={0,1001}_2\cdot 2^{11}.\]Порядок $110$ в двоичной системе счисления больше, чем $11$, поэтому найдем разность между порядками: ${110}_2-{11}_2={11}_2=3_{10}$. Сдвигаем мантиссу второго числа (с меньшим порядком) вправо на $3$ разряда:
\[{0,1001}_2\cdot 2^{11}={0,0001001}_2\cdot 2^{110}.\]Т.к. порядки обоих чисел теперь одинаковых, можно выполнить операцию суммирования, добавив ко второму числу необходимое количество нулей справа:

Рисунок 3.
В результате получили нормализованное число, т.е. никаких преобразований не требуется.
Умножение
При умножении двух нормализованных чисел их мантиссы умножаются и порядки складываются.
Алгоритм выполнения умножения нормализованных вещественных чисел $A$ и $B$:
-
Перемножить мантиссы чисел.
-
Вычислить порядок произведения $P_C=P_A+P_B$.
-
Нормализовать (если есть необходимость) мантиссу произведения (возможен сдвиг на $1$ разряд влево с одновременным уменьшением порядка результата на $1$).
Выполнить умножение нормализованных чисел:
\[\left({0,11101}_2\cdot 2^{101}\right)\cdot \left({0,1001}_2\cdot 2^{11}\right)={\left(0,11101\cdot 0,1001\right)}_2\cdot 2^{101+11}=\] \[={0,100000101}_2\cdot 2^{1000}.\]Выполнить умножение чисел $3,5$ и $8,25$ в двоичной системе счисления.
Переведем данные числа в двоичный код:
\[{3,5}_{10}={0000\ 0011,1}_2={0,111}_2\cdot 2^{10}.\] \[{8,25}_{10}={0000\ 1000,01}_2={0,100001}_2\cdot 2^{100};\]Получили нормализованный результат $0.11100111\ \cdot 2^{110}$.
Деление
При выполнении деления двух нормализованных чисел мантисса делимого делится на мантиссу делителя и из порядка делимого вычитается порядок делителя. Если результат получают не нормализованный, то его необходимо нормализовать.
При делении (если необходимо) меньшую мантиссу добавляют нулями.
Алгоритм выполнения деления нормализованных вещественных чисел $A$ и $B$:
-
Мантиссу делимого разделить на мантиссу делителя.
-
Вычислить порядок частного $P_C=P_A-P_B.$
-
Нормализовать мантиссу полученного числа (возможен сдвиг на $1$ разряд вправо с одновременным увеличением порядка результата на $1$).
Выполнить деление нормализованных чисел:
\[\left({0,1111}_2\cdot 2^{100}\right):\left({0,101}_2\cdot 2^{11}\right)={\left(0,1111:0,101\right)}_2\cdot 2^{100-11}=\] \[={1,1}_2\cdot 2^1={0,11}_2\cdot 2^{10}.\]Выполнить деление чисел $28,875$ и $3,5$ в двоичной системе счисления.
Переведем данные числа в двоичный код:
\[{28,875}_{10}={0001\ 1100,111}_2={0,11100111}_2\cdot 2^{101};\] \[{3,5}_{10}={0000\ 0011,1}_2={0,111}_2\cdot 2^{10}.\]При делении меньшую мантиссу добавим нулями:
В результате получили не нормализованное число, поэтому его мантиссу сдвигаем вправо на 1 разряд и увеличиваем порядок на $1$: ${1,00001}_2\cdot 2^{11}={0,100001}_2\cdot 2^{100}$.











