Графы
Структурируем информацию о дорогах в населенных пунктах: Солнцево, Ясное и Грибное.
«От пос. Васюки идут три дороги в Солнцево, Ягодное и Грибное. Между Грибным и Солнцевым и между Грибным и Ягодным также есть дороги. Есть дорога, идущая из Грибного в лес и возвращается обратно в Грибное».
Нарисуем схему дорог:
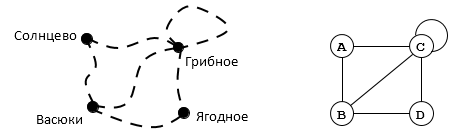
Рисунок 1.
В информатике такие схемы называются графами.
Граф – это набор узлов (вершин) и связей между ними (рёбер).
Информацию об узлах и связях обычно записывают в таблицу (матрицу).
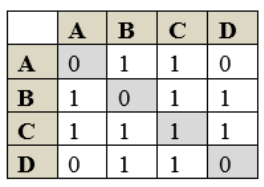
Рисунок 2.
Единица на пересечении строки и столбца означает наличие связи между узлами. Ноль говорит о том, что связи нет. Приведенная таблица называется матрицей смежности. Важно, что она симметрична относительно главной диагонали (серые клетки в таблице).
По условию есть дорога, идущая из Грибного в лес и возвращается обратно в Грибное, поэтому на пересечении строки $C$ и столбца $C$ поставлена единица и которая говорит о том, что в графе есть петля – ребро, которое начинается и заканчивается в одной и той же вершине.
Можно составить список смежности. Для каждого узла перечисляются все узлы, с которыми он связан. Для рассмотренного графа список смежности выглядит так:
\[(A (B, C), B (A, C, D), C (A, B, C, D), D (B, C)) \]Матрица смежности (и список смежности) не дают никакой информации о том, как именно расположены узлы друг относительно друга. Для таблицы, приведенной выше, возможны, например, такие варианты:
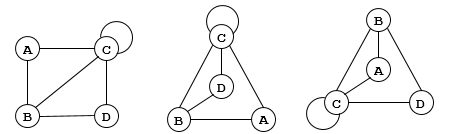
Рисунок 3.
В рассмотренном примере все узлы связаны, т.е. между любой парой узлов существует путь – последовательность ребер, по которым можно перейти из одного узла в другой, такой граф называется связным.
Теперь представим такую ситацию, что дороги Васюки – Солнцево, Васюки – Грибное и Грибное – Ягодное размыло дождем или завалило снегом так, что по ним не пройти. Тогда схема будет выглядеть следующим образом, как показано на схеме ниже.
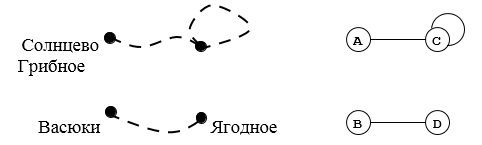
Рисунок 4.
Эту схему тоже можно считать графом, но в таком графе есть две несвязанные части, и каждая часть является связным графом. Такие части называют компонентами связности.
Если в примере с дорогами нам нужно знать еще и расстояния между поселками, то каждой связи нужно сопоставить вес (число).
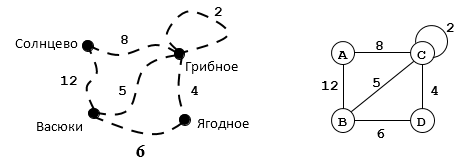
Рисунок 5.
Такой граф называется взвешенным, поскольку каждое ребро имеет свой вес. В реальных задачах это может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Для взвешенного графа в таблице записывается не $1$ или $0$, а вес ребра-длина дороги. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в нее условный код, например, $–1$. Такая таблица называется весовой матрицей, потому что содержит веса ребер. В данном случае она выглядит так:
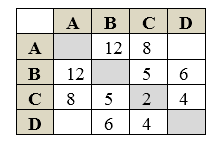
Рисунок 6.
Также как и матрица смежности, весовая матрица симметрична относительно диагонали. Две пустые ячейки говорят о том, что между узлами $A$ и $D$ нет связи.
Если в графе немного узлов, весовая матрица позволяет легко определить наилучший маршрут из одного узла в другой простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей (числа определяют стоимость поездки между соседними пунктами):
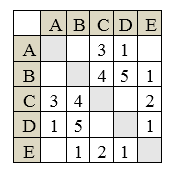
Рисунок 7.
Найдем наилучший путь из $A$ в $B$ – такой, при котором общая стоимость поездки минимальная. Сначала видим, что из пункта $A$ напрямую в $BB$ ехать нельзя, а можно ехать только в $C$ и $D$. Изобразим это на схеме:
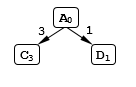
Рисунок 8.
Числа около каждого ребер показывают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла $A$.
Теперь разберем варианты дальнейшего движения из узла $C$ (узел $A$ уже не нужно рассматривать, так как мы из него пришли).
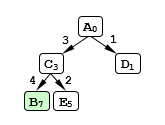
Рисунок 9.
Видим, что из $C$ сразу можно попасть в $B$, стоимость проезда в этом случае равна семи. Но, это может быть не самый лучший вариант, необходимо проверить еще путь через узел $E$. Действительно, оказывается, что стоимость можно сократить до шести:
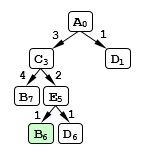
Рисунок 10.
Исследовать дальше маршрут, содержащий цепочку $ACED$, нет смысла, потому что его стоимость явно будет больше шести. Аналогично строим вторую часть схемы.
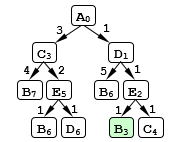
Рисунок 11.
Таким образом, оптимальный (наилучший) маршрут – $ADEB$, его стоимость равна трем.
Если для каждого ребра ещё указывать направление движения, то граф называется ориентированным (или коротко орграфом). Примерами таких дорог может быть модель с односторонним движением. Тогда матрица смежности и весовая матрица для орграфа уже не будут симметричными.












