Алгоритмы вычислительной геометрии

Общие сведения о вычислительной геометрии

Вычислительная геометрия является очень интересной и относительно молодой областью компьютерной науки, находящейся на стыке информатики и геометрии и сочетающей геометрические термины, идеи и модели с терминами, идеями и способами создания алгоритмов и структур данных.

Геометрические объекты, по существу, могут считаться зачатками алгоритмической науки. В самом деле, в задачах на создание на основании заданных геометрических объектов (точек, прямых, отрезков и окружностей), то есть, по исходным данным, необходимо сформировать иные геометрические объекты. Это означает, что выходные данные формируются при помощи фиксированного инструментального набора, то есть, базовых операций или примитивов, в качестве которых могут быть использованы, к примеру, циркуль и линейка, или только циркуль, или только линейка.

Изобретение компьютеров и далее бурный прогресс компьютерной науки, а именно, информатики, предоставило возможность объединения чисто геометрической сути задач на построение с аналитическим, то есть, вычислительным подходом к их решению. Это, со своей стороны, позволило прийти к возможности разрешения нового класса задач, которые и призвана решать вычислительная геометрия.

В таких задачах в качестве исходных данных выступают геометрические объекты, такие как, набор точек, совокупность отрезков, многоугольники, а в итоговом результате могут быть следующие моменты:

1. Ответы на вопросы об определенных связях между исследуемыми объектами (к примеру, есть ли пересечение у выбранных отрезков).
2. Перечень фактов, касающихся данных отношений (к примеру, перечень всех пар пересекающихся отрезков).
3. Формирование новых геометрических объектов (к примеру, самого маленького выпуклого многоугольника, который содержит необходимые точки).

При этом следует отметить, что как размеры исходных данных (количество исследуемых геометрических объектов), так и размеры итогового результата (перечня или новых геометрических объектов) могут являться произвольными и, обычно, достаточно объемными.

Вычислительная геометрия используется в большом количестве областей науки и техники, а именно:

• в компьютерной графике и визуализации,
• в компьютерном зрении и робототехнике,
• в географических информационных системах (ГИС),
• в системах автоматизированного проектирования (САПР),
• в компьютерном анализе и интерпретации данных (к примеру, в компьютерной томографии),
• в молекулярной биологии,
• в астрофизике.

Алгоритмы вычислительной геометрии

Вычислительная геометрия является разделом информатики, изучающим алгоритмы решения геометрических задач.

Отрезок, для которого определено, какой из его концов должен считаться началом, а какой считаться концом, именуется вектором. Каждую точку в пространстве тоже можно рассматривать как вектор, но подобный вектор считается нулевым. Начало и конец нулевого вектора являются совпадающими, и такой вектор не обладает каким-либо определенным направлением. Длиной ненулевого вектора AB является длина отрезка AB, как показано на рисунке ниже:

Рисунок 1. Вектор АВ. Автор24 — интернет-биржа студенческих работ

Соответственно, длина нулевого вектора равняется нулю.

Пара ненулевых векторов называется коллинеарной, когда они расположены на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD являются коллинеарными, и если при этом лучи AB и CD выступают как однонаправленные, то векторы AB и CD именуются сонаправленными, а если эти лучи не являются однонаправленными, то векторы AB и CD должны называться противоположно направленными. Нулевой вектор может считаться сонаправленным с любым из векторов.

Скалярным произведением векторов является число, которое равно произведению длин этих векторов на косинус угла между ними:

$(a, b) = |a||b|cos∠(a, b)$

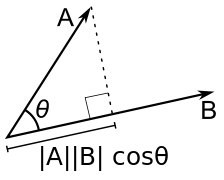
Рисунок 2. Угол между векторами a и b. Автор24 — интернет-биржа студенческих работ

В случае, когда векторы задаются при помощи своих координат $a(x_1, y_1), b(x_2, y_2)$, скалярное произведение равняется:

$(a, b) = x_1x_2 + y_1y_2$

Под псевдоскалярным или косым произведением векторов на плоскости понимается следующее число:

$[a, b] = |a||b|sinθ$

Здесь θ является углом вращения (против часовой стрелки) от a к b. В случае, кода хотя бы один из векторов a и b является нулевым, то следует полагать $[a, b] = 0$.

Когда векторы задаются при помощи своих координат $a(x_1, y_1), b(x_2, y_2)$, то косое произведение будет равно:

$ [a, b] = x_1y_2 — x_2y_1$

В геометрическом виде косое произведение векторов может быть представлено как ориентированная площадь параллелограмма, который натянут на эти вектора:

Рисунок 3. Параллелограмм. Автор24 — интернет-биржа студенческих работ

Косое произведение векторов в задачах вычислительной геометрии способно занять такое же почетное место, как рекурсия в комбинаторике. Оно является своего рода жемчужиной вычислительной геометрии. Практически все задачи вычислительной геометрии могут иметь более простое решение, в случае использования косого произведения вместо стандартного решения.

Рассмотрим конкретный пример, требуется по заданным трем числам a, b, c определить, может ли существовать треугольник с такими сторонами. Для нахождения решения, здесь следует просто проверить неравенство треугольника:

$a + b > c$,

$a + c > b$,

$b + c > a$.

Далее рассмотрим в качестве примера эту же задачу, но предположим, что треугольник определяется не сторонами, а координатами вершин.

Сначала может показаться, что решение является очевидным, а именно, следует вычислить стороны треугольника, после чего задача может быть сведена к предыдущей. Однако так как дистанция между двумя точками $A(x_1, y_1), B(x_2, y_2)$ должна вычисляться по формуле:

$√(x_1-x_2)^2+(y_1-y_2)^2$

то при извлечении квадратного корня вероятна потеря точности, что может плохо сказаться на проверке неравенства треугольника. Получается, когда треугольник определен координатами своих вершин, то выполнять вычисление длины его сторон и проверку неравенства треугольника не нужно. В этом варианте треугольник не существует тогда и только тогда, когда эти три точки расположены на одной прямой. А это можно легко проверить при помощи косого произведения векторов. Когда оно равняется нулю, то это означает, что векторы являются коллинеарными, что означает, что все три точки расположены на одной прямой.