Основные понятия
Деревом называется конечное множество, которое состоит из элементов, называемых узлами, для которых выполняются следующие правила:
- Узлы связаны отношением «исходный-порожденный».
- Порожденный узел не может стать исходным для своего предка, то есть отношение действует в одну сторону.
- Только один узел может не иметь исходного. Он называется корневым.
- Все узлы, кроме корневого, имеют один и только один исходный.
- Каждый узел может иметь неограниченное количество порожденных узлов.
Количество порожденных узлов данного узла называется его степенью.
Узел с нулевой степенью (не имеющий порожденных) называют листом или концевым узлом.
Максимальное значение степени, найденное среди всех узлов данного дерева, называют степенью дерева.
Если в некотором дереве существенен порядок следования для узлов, имеющих общий исходный узел, то такое дерево называется упорядоченным.
Упорядоченное дерево, имеющее степень не больше, чем 2, называют бинарным деревом или двоичным деревом.
Поиск по бинарному дереву
Бинарные деревья часто используются для поиска по базе данных. В качестве узлов дерева выбираются значения индексированного поля, по которому осуществляется поиск.
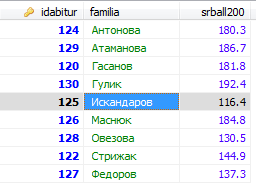
Рассмотрим следующую задачу. Дана таблица, где указаны фамилии абитуриентов и средние баллы аттестатов. Нужно найти средний балл абитуриента с фамилией Петров.
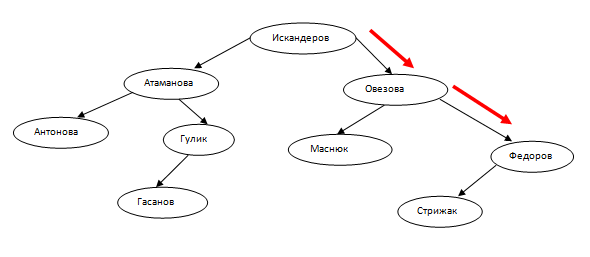
Ключом поиска в данном случае будет поле familia. При построении дерева список сначала делится пополам и корневым узлом становится ключ «Искандеров». Далее пополам делится список фамилий слева от корневого узла (ключ «Атаманова» )и справа от корневого узла (ключ «Овезова»). Узлы «Атаманова» и «Овезова» становятся порожденными для корневого узла. Далее пополам делятся списки фамилий, находящиеся слева и справа от ключей «Атаманова» и «Овезова» и т.д.
Поиск по построенному дереву осуществляется следующим образом:
- Проверяется равенство «Федоров»= «Искандеров». Оно ложно.
- Проверяется неравенство «Федоров» > «Искандеров». Оно истино, значит поиск переносится в правое поддерево корневого узла.
- Проверяется равенство «Овезова»= «Федоров». Оно ложно.
- Проверяется неравенство «Федоров»> «Овезова». Оно истино, значит поиск переносится в правое поддерево узла «Овезова».
- Проверяется равенство «Федоров»= «Федоров». Оно истинно, значит, поиск окончен.
Данные о среднем балле определяются в соответствии с найденным ключом.
Таким образом , при каждом переходе в новое поддерево, существенно сокращается область поиска. При прямом переборе фамилия Федоров была бы найдена за 9 шагов. При использовании поиска по дереву – за пять.
Поиск по В-дереву
Кроме поиска по бинарным деревьям часто применяется поиск по В-деревьям.
В-деревом n-го порядка называется дерево, обладающее следующими свойствами:
- Каждый узел содержит не более 2n ключей;
- Каждый узел, кроме корневого, содержит не менее n ключей;
- Если внутренний узел (не являющийся листом) содержит m ключей, то у него имеется m+1 порожденных узлов.
- Все листья находятся на одном уровне.
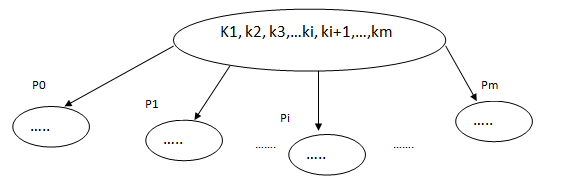
Поиск по такому дереву осуществляется следующим образом. Пусть нужно найти ключ К. Имеется узел c ключами k1,k2,…km и порожденные им узлы p0, p1,…pm
- Сначала происходит поиск ключа в корневом узле. Если ключ там обнаруживается, то поиск завершается.
- Если ключ К не обнаруживается в корневом узле, то происходит последовательное сравнение ключа К с ключами данного узла.
- Если найдутся такие ключи ki и ki+1, что ki , то поиск переносится в узел pi
- Если К>km, то поиск переносится в узел pm.
- Если K , то поиск переносится в узел p0.
- Алгоритм повторяется сначала для выбранного узла.
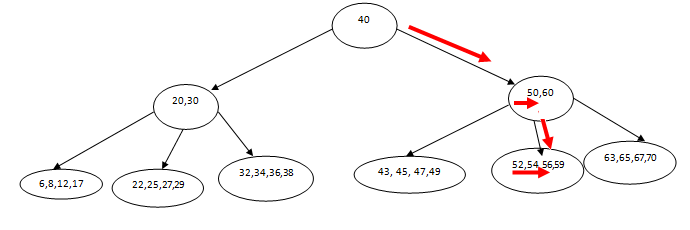
На рисунке приведен пример В-дерева второго порядка.
Чтобы найти в этом дереве ключ 56 нужно выполнить следующий алгоритм:
- Проверить утверждение 40=56. Оно ложно, поэтому поиск продолжается.
- Проверить утверждение 40
- Последовательно проверить утверждения 50=56 и 60=56. Оба утверждения ложны, поэтому нужно искать следующий порожденный узел для поиска.
- Найти ключи, между которыми находится искомый: 50
- Последовательным сравнением найти ключ 56 в выбранном узле.