Функция f(x) является непрерывной в точке а, если выполняются следующие условия:
- f(а) определена
- $\mathop{\lim }\limits_{x\to 0} f(x)$ существует
- $\mathop{\lim }\limits_{x\to 0} f(x)=f(a)$
Функция непрерывна на интервале (а, b) тогда и только тогда, когда она непрерывна во всех точках данного интервала.
Функция называется непрерывной (рис.1), если она непрерывна на всем промежутке $(-∞; +∞)$.
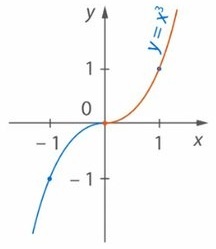Непрерывная функция">
Рисунок 1. Непрерывная функция
Определение непрерывности фактически повторяет определение предела функции в данной точке.
Другими словами, функция f непрерывна в точке a, предельной для множества D, если f имеет предел в точке a, и этот предел совпадает со значением функции f(a).
Статья: Непрерывность функций
Является ли функция непрерывной в точке а?
\[f(x)=x^{2} -9x+1\]Решение:
- Найдем предел функции \[\mathop{\lim }\limits_{x\to 0} x^{2} -9x+1=a^{2} -9a+1\]
- По условию непрерывности \[\mathop{\lim }\limits_{x\to 0} f(x)=f(a)\]
Является ли функция непрерывной?
\[f(x)=\left\{\begin{array}{cc} {\frac{\sin x}{x} } & {x\ne 0} \\ {1} & {x=0} \end{array}\right. \]Решение:
Проверим функцию на выполнимость условий определения 1
- f(0) = 1 -- значит функция определена;
- $\mathop{\lim }\limits_{x\to 0} \frac{\sin x}{x} =1$ - общий предел существует;
- $\mathop{\lim }\limits_{x\to 0} \frac{\sin x}{x} =f(0)$ - условие непрерывности выполнено.
Поскольку все условия выполнимы, функция является непрерывной в точке = 0.
Является ли функция непрерывной?
\[f(x)=\left\{\begin{array}{cc} {\frac{\cos 5x}{x} } & {x\ne 0} \\ {3} & {x=0} \end{array}\right. \]Решение:
Проверим функцию на выполнимость условий определения 1
- f(0) = 3 -- значит функция определена;
- $\mathop{\lim }\limits_{x\to 0} \frac{\cos 5x}{x} =\left\langle \frac{0}{0} \right\rangle =\mathop{\lim }\limits_{x\to 0} \frac{\left(\cos 5x\right)`}{\left(x\right)`} =\mathop{\lim }\limits_{x\to 0} \frac{5\sin 5x}{1} =5\mathop{\lim }\limits_{x\to 0} \sin 5x=5$
- $\mathop{\lim }\limits_{x\to 0} \frac{\cos 5x}{x} \ne f(0)$
Поскольку последнее условие не выполнено в точке 0 -- функция имеет разрыв.
Свойства непрерывности носят локальный и глобальный характер:
Локальные свойства непрерывности
- Непрерывная в точке функция является ограниченной в ее окрестности;
- Для функции непрерывной в точке а, при f(a) $>$ 0 (или f(a) $
- Если функции f(x) и g(x) непрерывны в точке х = а, то в этой точке непрерывны и такие функции как:
- Если функции f(x) и g(x) непрерывны в точке х = а и g(а) ≠ 0, то в точке х = а будет непрерывной также и функция f(x)/g(x);
- Если одна функция непрерывна в окрестности а, а другая в окрестности b, то их композиция непрерывна в точке а.
f(x) + g(x), f(x) -- g(x), f(x) • g(x);
Глобальные свойства непрерывности
- Функция равномерно непрерывная на любом множестве или отрезке;
- Функция непрерывная на любом множестве или отрезке всегда ограниченна данным множеством и достигает минимальных и минимальных значений на нем;
- Область значений непрерывной на отрезке функции f является отрезок [minf; maxf];
- Если функция f непрерывна на отрезке [a, b] и выполняется условие f(a)*f(b) $>$ 0, то на отрезке обязательно найдется такая точка в которой функция обратится в 0;
- Если функция f непрерывна на отрезке [a, b] и выполняется условие f(a) $
- Если функция f непрерывна на отрезке [a, b] и выполняется условие f(a) $>$ c $>$ f(b), то на отрезке обязательно найдется такая точка в которой функция обратится в точку с;
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна;
- Монотонная функция может быть непрерывной на отрезке, только если область ее значений ограничена f(a) и f(b);
- Если две функции непрерывны на отрезке, причем одна из них больше другой, то обязательно найдется такое значение на данном промежутке, при котором функции будут равны.
