Для начала напомним следующие определения:
Случайная величина называется двумерной, если она определяется двумя числами и обозначается $(X,Y)$.
Для одномерной случайной величины $X$ функцией распределения называется функция, удовлетворяющая равенству
\[F\left(x\right)=P(XВведем теперь аналогичное определение для функции распределения двумерной случайной величины $(X,Y)$.
Для двумерной случайной величины $(X,Y)$ интегральной функцией распределения называется функция, удовлетворяющая равенству
\[F\left(x,y\right)=P(XГеометрически данное определение можно истолковать следующим образом: интегральная функция распределения геометрически определяет вероятность попадания случайной величины $(X,Y)$ в бесконечный квадрат, правая верхняя вершина которого лежит в точке $(x,y)$ (рис. 1).
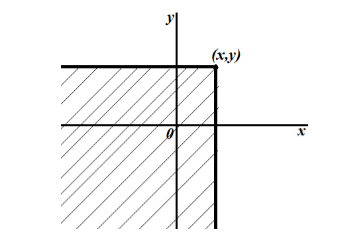
Рисунок 1. Геометрическое изображение функции $F(x)$.
Отметим несколько свойств функции распределения двумерной случайной величины:
Свойство 1: Все значения функции распределения лежат в промежутке $[0,1]$:
\[0\le F(x,y)\le 1\]Свойство 2: Функция распределения не убывает по каждой из своих компонент:
\[F\left(x_2,y\right)\ge F\left(x_1,y\right),\ если\ x_2Это свойство непосредственно следует из случая с одномерной случайной величиной.Свойство 3: Если хотя бы одна из переменных $x$ или $y$ стремится к $-\infty $, то сама функция распределения стремится к нулю:
\[F\left(-\infty ,y\right)=F\left(x,-\infty \right)=F\left(-\infty ,-\infty \right)=0\]Это следует из того, что события $(X
Свойство 4: Если обе переменные $x$ и $y$ стремятся к $+\infty $, то сама функция распределения стремится к единице:
\[F\left(+\infty ,+\infty \right)=1\]Это следует из того, что события $(X
Свойство 5: Если одна из переменных функции распределения стремится к $+\infty $, то функция распределения двумерной величины становится функцией распределения одномерной случайной величины, которая не стремится к $+\infty $.
\[F\left(+\infty ,y\right)=F\left(y\right)=P(YЭто свойство также следует из того, что события $(XПлотность распределения двумерной случайной величины.
С понятием функции распределения двумерной случайной величины тесно связано понятие плотности двумерной случайной величины. Придадим значениям $x\ и\ y$ двумерной случайной величины приращения $\triangle x$ и $\triangle y$.
Определение 4: Функция $\varphi (x,y)$ называется плотностью распределения двумерной случайной величины $(X,Y)$, если, с точностью до бесконечно малых высшего порядка относительно $\triangle p=\sqrt{{\triangle x}^2+{\triangle y}^2}$, выполняется равенство:
\[P(xГеометрически выражение $P(x
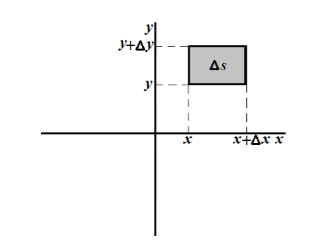
Обозначим этот прямоугольник через $\triangle s$. Тогда равенство в определении плотности распределения можно записать следующим образом:
\[P((X,Y)\in \triangle )\approx \varphi (x,y)\triangle s\]Отметим, что функция распределения и функция плотности распределения двумерной случайной величины, аналогично одномерному случаю, связаны по формуле:
\[F\left(x,y\right)=\int\limits^x_{-\infty }{\int\limits^y_{-\infty }{\varphi \left(t,z\right)dtdz}}\]Функция распределения дискретной двумерной случайной величины
Пусть случайная величина $(X,Y)$ является дискретной. И пусть для нее дан закон её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:
\[F\left(x,y\right)=P\left(XФункция распределения непрерывной случайной величиныПусть случайная величина $(X,Y)$ теперь является непрерывной. И пусть для нее дана плотность её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:
\[F\left(x,y\right)=\int\limits^x_{-\infty }{\int\limits^y_{-\infty }{\varphi \left(t,z\right)dtdz}}\]где $\varphi \left(x,y\right)$ - плотность непрерывной случайной величины $(X,Y)$.
Пример задачи на нахождение функции распределения двумерной случайной величины
Вероятность попадания футбольным игроком по воротам при одном ударе равна $0,8$. Найти интегральную функцию распределения числа попаданий и промахов при этом ударе.
Решение.
Составим сначала закон распределения данной случайной величины. Пусть $X$ число попаданий по воротам, а $Y$ - число промахов по воротам. Вероятность промаха равна $1-0,8=0,2$. Из этого всего получаем следующий закон распределения случайной величины $(X,Y)$:

Рисунок 3.
Замечание: по главной диагонали нули, так как нельзя одновременно и попасть и промахнуться.
Из полученного закона, очевидно, что функция распределения имеет вид:
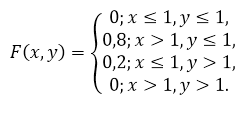
Рисунок 4.












