Вероятность перехода
Общая задача нахождения состояний квантовой системы, например, атома в поле электромагнитной волны в дипольном приближении - это решение нестационарного уравнения Шредингера при использовании дипольного приближения:
где оператор взаимодействия ($\hat{W}\left(\overrightarrow{r},t\right)$) определяется как:
Допустим, что система при t=0 (начальный момент времени) пребывает в стационарном состоянии и имеет невозмущенный атомный оператор Гамильтона ${\hat{H}}_0$ и:
где $\Psi_i$ -- функция, которая удовлетворяет стационарному уравнению Шредингера вида:
Система собственных функций ${\hat{H}}_0$ является полной, что значит -- волновая функция любого состояния $\Psi\left(\overrightarrow{r},t\right)$ может быть выражена как линейная комбинация собственных функций невозмущенного оператора Гамильтона:
Приняв во внимание выражение (5) можно представить уравнение (3) в виде:
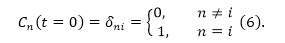
Рисунок 1.
Коэффициенты $C_n\left(t\right)$ -- это амплитуды вероятности найти систему в момент времени $t$ в стационарном состоянии $n$. В процессе воздействия на квантовую систему со стороны поля электромагнитной волны переходы между состояниями оператора Гамильтона для атома происходят с вероятность равной ${\left|C_n\left(t\right)\right|}^2$. Так, амплитуда вероятности перехода из начального состояния $\left|\left.i\right\rangle \right.$ в конечное состояние $\left|\left.s\right\rangle \right.$ за время $t$, если возмущение задано оператором $\hat{W}\left(\overrightarrow{r},t\right)$ в первом порядке возмущений будет равна:
где ${\omega }_{si}=\frac{E_s-E_i}{\hbar }$ - частота перехода. Если учесть выражение (2), то уравнение (7) можно преобразовать к виду:
где $d_{si}$ -- матричный элемент оператора z --проекции дипольного момента системы. $E\left(t\right)=E_0{cos \left(щt\right)\ }$ - электрическое поле волны. Применяем формулу:
получаем:
при этом ${\omega }_{si}$ может быть и больше, и меньше нуля.
Выражение для вероятности электромагнитного перехода из состояния $\left|\left.i\right\rangle \right.$ в конечное состояние $\left|\left.s\right\rangle \right.$ за время $t$ вблизи от резонанса при переходе с поглощением энергии можно определить как:
где $\triangle \omega =\omega_{si}-\omega.$
Разрешенные и запрещенные переходы
Если выполняется равенство вида:
то переход называют разрешенным. В том случае, если:
переход является запрещенным. Так как если $d_{si}=0$, то вероятность перехода оказывается равной нулю даже в электромагнитном поле, которое является сильным (для электрического дипольного приближения в низком порядке теории возмущений). Запрещенный в электрическом дипольном приближении переход может стать разрешенным в высоких порядках разложения по мультиполям. Следует отметить, что если имеем дело в исследуемом случае с запрещенным переходом - это не значит, что он не возможен в принципе. Лучше сказать, что он является маловероятным, в сравнении с разрешенными переходами в электрическом дипольном приближении.
Понятие о правилах отбора
Соотношения между квантовыми числами в начальном и конечном состояниях квантовой системы, при которых электромагнитные переходы становятся возможными, называют правилами отбора.
Можно привести несколько примеров формулировок правил отбора для разных квантовых систем.
-
Правила отбора для переходов в линейном гармоническом осцилляторе. Так, электромагнитные переходы возможны только между парой соседних состояний гармонического осциллятора. Эффективное взаимодействие осциллятора с внешним полем электромагнитной волны возможно только, если частота осциллятора совпадает с частотой внешнего поля.
-
Правила отбора для заряженной частицы находящейся в поле с центральной симметрией. По магнитному квантовому числу ($m$) правило отбора запишется как:
то есть в случае электромагнитных переходов магнитное квантовое число изменяется не 1 или не изменяется.
При электрическом дипольном переходе орбитальное квантовое число изменяется не один:
Допустим, что в процесс перехода сопровождается излучением (поглощением) фотона. Спин фотона равен единице. Выражение (14) является представлением закона сохранения момента количества движения в системе атом -- электромагнитное поле. Фотон унесет при излучении единичный момент. При этом проекция может изменить значение на единицу или не менять его вовсе. В случае $\triangle m=0$ испускаются фотоны, имеющие линейную поляризацию. При $\triangle m=\pm 1$ испускаются фотоны с круговой поляризацией.
Ограничений на изменение главного квантового числа нет. Правила отбора (13) - (14) выполняются для переходов в поле с центральной симметрией, например, в атоме водорода.
Полные правила отбора учитывают существование спинового механического момента электрона. Оператор взаимодействия с электромагнитным полем в дипольном приближении не зависит от спиновых переменных, можно записать:
Правило отбора для изменения полного механического момента атома ($j$) и его проекции формулируют как:
Для квантового числа $j$ имеем:
Покажите, что в общем случае теорию возмущений при рассмотрении взаимодействия атома с полем электромагнитной волны можно применять, только если воздействие поля на атом ограничено по времени.
Решение:
Запишем выражение для амплитуды вероятности перехода из начального состояния $\left|\left.i\right\rangle \right.$ в конечное состояние $\left|\left.s\right\rangle \right.$ за время $t$:
\[C^{\left(1\right)}_s\left(t\right)=\frac{id_{si}E_0}{2\hbar }\left(\frac{e^{i\left({\omega }_{si}-\omega \right)t}-1}{i\left({\omega }_{si}-\omega \right)}+\frac{e^{i\left({\omega }_{si}+\omega \right)t}-1}{i\left({\omega }_{si}+\omega \right)}\right)\left(1.1\right).\]Рассмотрим переход, который происходит около резонансной частоты ($\omega \approx \left|{\omega }_{si}\right|$) с поглощением энергии внешнего поля. Тогда можно пренебречь $\frac{e^{i\left({\omega }_{si}+\omega \right)t}-1}{i\left({\omega }_{si}+\omega \right)}$ в сравнении с $\frac{e^{i\left({\omega }_{si}-\omega \right)t}-1}{i\left({\omega }_{si}-\omega \right)}$ в выражении (1.1), имеем:
\[C^{\left(1\right)}_s\left(t\right)=\frac{id_{si}E_0}{2\hbar }\left(\frac{e^{i\left({\omega }_{si}-\omega \right)t}-1}{i\left({\omega }_{si}-\omega \right)}\right)\left(1.2\right).\]Введем обозначение: $\triangle \omega ={\omega }_{si}-\omega $, тогда выражение (1.2) перепишем в виде:
\[C^{\left(1\right)}_s\left(t\right)=\frac{id_{si}E_0}{2\hbar }e^{i\frac{\triangle \omega t}{2}}\frac{{\sin \left(\frac{\triangle \omega t}{2}\right)\ }}{\frac{\triangle \omega }{2}}\left(1.3\right).\]При этом вероятность перехода ($P_{si}$) из состояния \textit{i} в состояние \textit{s} равна:
\[P_{si}\left(t\right)={\left|{C_s}^{\left(1\right)}\left(t\right)\right|}^2=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}\frac{{sin}^2\left(\frac{\triangle \omega t}{2}\right)}{{\left(\frac{\triangle \omega }{2}\right)}^2}\left(1.4\right).\]Так как теория возмущений применима только при условии $P_{si}\ll 1,\ $для резонанса (при $\triangle \omega =0$) из (1.4) получим:
\[P_{si}\left(t\right)=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}\frac{{sin}^2\left(\frac{\triangle \omega t}{2}\right)}{{\left(\frac{\triangle \omega}{2}\right)}^2}\approx t^2(1.5)\]Выражение (1.5) показывает, что условие $P_{si}\ll 1$ выполняется на ограниченном интервале времени.
Что и следовало показать.
Чему равна вероятность перехода в единицу времени для $t\to \infty $, но малых вероятностях перехода ($p_{si}$)?
Решение:
Для решения задачи применим формулу:
\[{\mathop{\lim }_{t\to \infty } \frac{{sin}^2\alpha t}{{\alpha }^2t}\ }=\pi \delta \left(\alpha \right)\left(2.1\right),\]где $\delta \left(\alpha \right)$ --дельта функция. Из выражения, полученного в примере 1 (1.4) получим:
\[P_{si}\left(t\right)=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}2\pi \delta \left({\omega }_{si}-\omega \right)t\left(2.2\right).\]Выражение (2.2) показывает, что при $t\to \infty $ вероятность перехода увеличивается прямо пропорционально времени. Величину $p_{si}=\frac{P_{si}}{t}$ называют вероятностью перехода в единицу времени, она будет равна:
\[p_{si}=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}2\pi \delta\left(\omega_{si}-\omega\right)=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}2\pi \delta \left(E_s-E_i-\hbar \omega \right).\]Ответ: $p_{si}=\frac{{\left|d_{si}\right|}^2E^2_0}{4{\hbar }^2}2\omega \delta\left(E_s-E_i-\hbar \omega\right).$













