Определение векторного потенциала
Одно из основных уравнений магнитостатики имеет вид:
Решение этого уравнения может быть определено как:
где вектор $\overrightarrow{A\ }$ называют векторным потенциалом магнитного поля. Из векторного анализа хорошо известно тождество:
Многозначность векторного потенциала
Поле, в котором известен вектор индукции ($\overrightarrow{B}$) может быть описано несколькими векторными потенциалами. Покажем, что если потенциал $\overrightarrow{A\ }$описывает поле с индукцией $\overrightarrow{B}$, то и другой потенциал $\overrightarrow{A'}$, в виде:
при любом $\varkappa$, описывает то же самое поле. Проведем операцию rot уравнения (4), получим:
так как $rot\left(grad\varkappa \right)\equiv 0.$
Многозначность векторного потенциала магнитного поля эквивалентна неоднозначности скалярного потенциала электростатического поля. Разница состоит в том, что потенциал в электростатике определяется с точностью до произвольной постоянной, тогда как векторный потенциал магнитостатического поля, определятся с точностью до произвольной функции определённого класса. Произвольность в выборе векторного потенциала показывает, что векторный потенциал имеет вспомогательное значение. Он не может быть измерен в эксперименте.
Калибровка векторного потенциала
В магнитостатике в качестве калибровочного условия для векторного потенциала используют уравнение:
Уравнение (6) называют условием калибровки потенциала.
Уравнение для векторного потенциала
Запишем теорему о циркуляции вектора $\overrightarrow{B}$ в дифференциальной форме:
где $\overrightarrow{j}$ -- вектор плотности тока, ${\mu }_0$ -- магнитная постоянная. Подставим (2) в уравнение циркуляции (7), получим:
Преобразуем выражение $rotrot\overrightarrow{A}$ согласно известному из векторного анализа соотношению:
$graddiv\overrightarrow{A}=0\ (из\ условия\ калибровки\ (6)\ ),$ следовательно, уравнение (8) приобретет вид:
В координатном представлении уравнение (10) запишется в форме:
В системе уравнений (11) мы получили, что каждая компонента векторного потенциала подчиняется уравнению Пуассона. Следовательно, можно предположить, что решение уравнений (11) можно записать в виде:
где $r$ -- радиус вектор, который проведен из элемента тока в точку наблюдения. В векторной форме (12) запишем как:
Для тока в прямолинейном проводнике (линейного тока), можно записать, что векторный потенциал равен:
где $L_i$- контуры токов, $I_i$- силы токов в контурах.
Если найден векторный потенциал, то используя его определение можно отыскать соответствующую ему индукцию магнитного поля. Введение векторного потенциала существенно облегчает изучение магнитного поля постоянных токов.
Задание: Найдите вектор-потенциал магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I.
Решение:
Пусть начало координат находится в середине, рассматриваемого участка с током (рис.1).
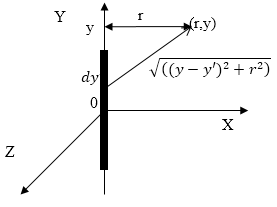
Рис. 1
Магнитное поле прямолинейного проводника с током обладает цилиндрической симметрией, следовательно. Координаты точки в данной плоскости характеризуются расстоянием r от оси Y и координатой y. В качестве основы для решения задачи используем выражение:
\[\overrightarrow{A}=\frac{{\mu }_0}{4\pi }\int\limits_L{\frac{I}{r}}d\overrightarrow{l}=\frac{{\mu }_0}{4\pi }\sum\limits_i{I_i}\int\limits_{L_i}{\frac{d\overrightarrow{l}}{r}}\left(1.1\right).\]Из (1.1) следует, что не равна нулю только компонента $A_y\ne 0$. ($A_x=0{,A}_z=0$) так как ток течет только по оси Y. В таком случае запишем:
\[{A=A}_y=\frac{\mu_0I}{4 \pi}\int\limits^{\frac{L}{2}}_{-\frac{L}{2}}{\frac{dy'}{\sqrt{{\left(y-y'\right)}^2+r^2}}}=\frac{\mu_0I}{4 \pi}ln\left(\frac{-y+\frac{L}{2}+\sqrt{{\left(y-\frac{L}{2}\right)}^2+r^2}}{-\left(y+\frac{L}{2}\right)+\sqrt{{\left(y+\frac{L}{2}\right)}^2+r^2}}\right)(1.2).\]Для бесконечно длинного проводника векторный магнитный потенциал равен:
\[L\to \infty ;А=\frac{{\mu }_0I}{4\pi }lnr+const.\]Ответ: A=$\frac{{\mu }_0I}{4\pi }ln\left(\frac{-y+\frac{L}{2}+\sqrt{{\left(y-\frac{L}{2}\right)}^2+r^2}}{-\left(y+\frac{L}{2}\right)+\sqrt{{\left(y+\frac{L}{2}\right)}^2+r^2}}\right).$
Задание: Используя результат решения задачи «Пример 1». Найдите индукцию магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I. (рис.1).
Решение:
Из симметрии магнитного поля данного проводника с током индукцию достаточно вычислить в точках плоскости XY. Будем вычислять ее по формуле:
\[\overrightarrow{B}=rot\overrightarrow{A\ }\left(2.1\right),\]где из предыдущей задачи имеем:
\[A_y=\frac{\mu_0I}{4 \pi}ln\left(\frac{-y+\frac{L}{2}+\sqrt{{\left(y-\frac{L}{2}\right)}^2+r^2}}{-\left(y+\frac{L}{2}\right)+\sqrt{{\left(y+\frac{L}{2}\right)}^2+r^2}}\right)(2.2).\]Удобнее индукцию, опять таки из соображений симметрии поля, записать в цилиндрических координатах. При этом будем иметь, что не равна нулю только проекция $B_{\varphi }$, где $\varphi $ -- угол цилиндрической системы координат. При этом можно записать, что:
\[B_{\varphi }=-\frac{\partial A_y}{\partial r}\left(2.3\right).\]На рис. 1 на плоскости XY $компонента\ B_{\varphi }$ направлена перпендикулярно плоскости в против оси Z. Подставим (2.2) в (2.3), получим:
\[B_{\varphi }=\frac{{\mu }_0I}{4\pi }\left\{\frac{-y+\frac{L}{2}}{\sqrt{{\left(y-\frac{L}{2}\right)}^2+r^2}}+\frac{y+\frac{L}{2}}{\sqrt{{\left(y+\frac{L}{2}\right)}^2+r^2}}\right\}.\]Для бесконечного прямолинейного проводника имеем:
\[L\to \infty ;\ B_{\varphi }=\frac{{\mu }_0I}{2\pi r}.\]Ответ: B=$B_{\varphi }=\frac{{\mu }_0I}{4\pi }\left\{\frac{-y+\frac{L}{2}}{\sqrt{{\left(y-\frac{L}{2}\right)}^2+r^2}}+\frac{y+\frac{L}{2}}{\sqrt{{\left(y+\frac{L}{2}\right)}^2+r^2}}\right\}.$












