Самым простым, после атома водорода является атом гелия. Его атомная оболочка содержит два электрона. Попытки описать данный атом используя квантовую теорию Бора стали несостоятельными.
- Теория Бора не дает возможность учесть обменную энергию, которая играет значимую роль в многоэлектронных атомах.
- Данная теория не учитывает существование спина у электрона.
Уравнение Шредингера для атома гелия
Перемещение частицы в потенциальном поле можно описать при помощи уравнения Шредингера:
где гамильтониан частицы имеет вид:
Подробная запись уравнения (1) для одного электрона принимает вид:
Атом гелия имеет два электрона. Полная энергия системы сложится из:
-
кинетических энергий электронов в атоме:
\[E_{k1}=\frac{p^2_1}{2m_e};\ E_{k2}=\frac{p^2_2}{2m_e}\left(4\right).\] -
потенциальных энергий 2 электронов в одном поле ядра атома гелия: $E_{p1}\left({\overrightarrow{r}}_1\right)и\ E_{p2}\left({\overrightarrow{r}}_2\right),$ где ${\overrightarrow{r}}_1$ -- радиус -- вектор первого электрона, ${\overrightarrow{r}}_2$ -- радиус-вектор второго электрона.
-
энергии взаимодействия электронов:
\[E_{p12}=E_{p21}=\frac{{q_e}^2}{4\pi {\varepsilon }_0\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}\left(5\right),\]\end{enumerate}
где $r_{12}=\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|$ -- расстояние между электронами. В таком случае оператор Гамильтона для атома гелия в уравнении (1) можно представить как:
При этом волновая функция зависит от шести переменных (координат 2 электронов). Так, уравнение (3) предстанет в виде:
где ${{\nabla }_1}^2=\frac{\Psi^2}{\Psi x^2_1}+\frac{\Psi^2}{\Psi y^2_1}+\frac{\Psi^2}{?z^2_1};{\Psi_2}^2=\frac{\Psi^2}{\Psi x^2_2}+\frac{\Psi^2}{\Psi y^2_2}+\frac{\Psi^2}{\Psi z^2_2}.\ $
Выражение вида ${\left|\Psi({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)\right|}^2$является плотностью вероятности обнаружить первый и второй электроны в точках, которые определены радиус-векторами ${\overrightarrow{r}}_1\ $(первый электрон), ${\overrightarrow{r}}_2$ (второй электрон).
Цель задачи в нахождении собственных значений и собственных функций уравнения (7). При этом требования, которые накладываются на собственную функцию остаются такими же, как и для одного электрона. Точное решение данного уравнения крайне сложная задача. Самым часто используемым приближением при решении уравнения (7) является представление волновой функции в виде произведения функций для каждого электрона в отдельности, которая изменяет знак при одновременной перестановке координат и спиновых переменных. Так для нерелятивистского случая волновую функцию для двух электронов записывают как:
где $\Psi_a\left(1\right)$-- волновая функция первого электрона, который находится в состоянии$\ a$ (при этом считают, что $E_a(1)$ -- энергия первого электрона в состоянии $a$, $\Psi_b\left(2\right)$ -- волновая функция второго электрона в состоянии $b$.
Если ${\varphi }_a\left({\overrightarrow{r}}_1\right)$ -- волновая функция, которая описывает положение электрона в пространстве, то полная волновая функция с учетом спина имеет вид:
где $\gamma $ -- спиновая функция электрона. Функцию для двух электронов запишем как:
Знаки $\pm $ соответствуют симметричной (или антисимметричной функциям). Они выбираются согласованно. Антисимметричная спиновая функция соответствует состоянию, при котором полный спин равен нулю $(S=0)$ (синглет). Ее можно выразить через одночастичные ортонормированные спиновые функции, которые определяют состояние одного электрона:
Для триплетного состояния (при $S=1$) ортонормированные спиновые функции можно представить как:
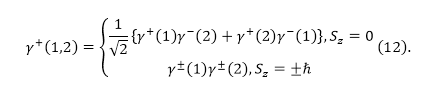
Рисунок 1.
Для координатной функции можно записать:
здесь индексы $1$ и $2$ определяют одночастичные состояния электронов.
В основном состоянии атома гелия координатная волновая функция должна быть симметричной по отношению к перестановке. Координатные волновые функции, для отдельных электронов в основном состоянии атома гелия, из-за высокой симметрии состояния, выбирают одинаковыми и самыми простыми, это означает, что ограничиваются $s-$ состоянием. Радиальные функции выбирают так, чтобы они не были равны нулю при конечных расстояниях. Основное состояние атома гелия описывается электронной конфигурацией: $1s^2.$
Задание: Найдите в нулевом приближении энергию полной ионизации, если атом гелия находится в основном состоянии.
Решение:
Искомая энергия ионизации равна работе по удалению на бесконечность $2$ электронов атома гелия.
Сложность задачи об атоме гелия вызвана присутствием в уравнении (7) члена $E_{p12}\left(\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|\right)\Psi,\ $который зависит от координат обоих электронов. Если рассматривать выражение $E_{p12}\left(\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|\right)\Psi$ как малую поправку, то в нулевом приближении ее можно не учитывать. Тогда задача в нулевом приближении сведется к задачам поиска собственных функций и собственных значений одноэлектронного водородоподобного атома. Такое решение хорошо известно.
Так, работа по удалению электрона в бесконечность из атома водорода, который находится в основном состоянии, равна:
\[A=\frac{m_e{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}\left(1.1\right).\]Для ионизированного один раз атома гелия такая работа будет в $Z^2$ раз больше. Если удаляют два электрона, то энергию ионизации в нулевом приближении для атома гелия находящегося в основном состоянии, можно найти как:
\[{E_i}^0=2Z^2\frac{m_e{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}.\]Проедем вычисления:
\[{E_i}^0=2\cdot 2^2\frac{9,1\cdot {10}^{-31}\cdot {\left({1,6\cdot 10}^{-19}\right)}^4}{32{\cdot 3,14}^2\cdot {\left(8,85\cdot {10}^{-12}\right)}^2{\left(1,05\cdot {10}^{-34}\right)}^2}\approx 108,3\ \left(эВ\right).\]Ответ: ${E_i}^0\approx 108,3эВ.\ $
Задание: Объясните, почему в нулевом приближении разница между вычисленным значением энергии полной ионизации атома гелия в основном состоянии и экспериментальным значением для той же величины ошибка составляет около $40\%$. Согласно экспериментальным данным энергия полной ионизации атома гелия составляет $78,98$ эВ.
Решение:
Разница в энергии ионизации возникает, так как в нулевом приближении не учитывается взаимодействие электронов. Зная волновую функцию в нулевом приближении ($\Psi^0$) можно применить формулу:
\[E^1=\int{\Psi^{0*}{\hat{E}}_{12}}\Psi^0dV_1dV_2\left(2.1\right),\]где ${\hat{E}}_{12}=\frac{{q_e}^2}{4\pi {\varepsilon }_0\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}$ -- часть оператора Гамильтона, которая учитывает взаимодействие между электронами и найти поправку к полной энергии ионизации атома гелия в первом приближении. Вычисления дают:
\[E_i=\left({E_i}^0+{E_i}^1\right)=\left(2Z^2-\frac{5}{4}Z\right)\frac{m_e{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}\approx 74,46\ \left(эB\right).\]












